A circuit made up of a resistor and capacitor causes a phase shift between the current and voltage. In this lab, you will be able to observe this effect and use it to measure the magnitude and angle of impedance, equivalent series resistance, and capacitance.
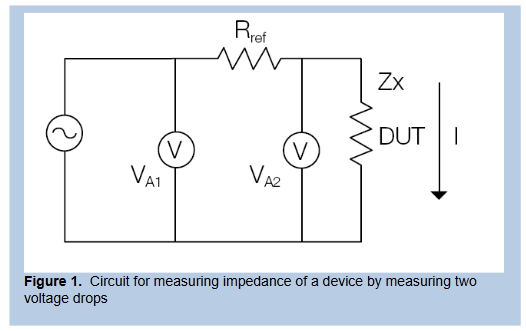
The Principle Behind Impedance Measurement
Impedance is the total opposition to current flow in an alternating current circuit. It is made up of resistance (real) and reactance (imaginary) and is usually represented in complex notation as Z = R + jX, where R is the resistance and X is the reactance.
Real-world components are made up of wires, connections,conductors and dielectric materials. These elements combine to make up the impedance characteristics of the component, and this impedance changes based on the test signal frequency and voltage level, the presence of a DC bias voltage or current and environmental factors such as operating temperatures or altitude. Of these potential influences the test signal frequency is often the most significant factor.
Unlike ideal components, real components are not purely inductive or capacitive. All components have a series resistance, which is the R parameter in its impedance. But they also have multiple contributors to their reactance. For example, a capacitor has a series inductance that becomes more apparent at high frequencies. When we measure a real capacitor, the series inductance (ESL) will impact the capacitance reading, but we won't be able to measure it as a separate, distinct component.
The impedance measuring technique used in this lab uses two voltage waveforms at different points to calculate the unknown impedance, Zx. as shown in Figure 1. Equation 1 shows how the circuit can be used to find Zx.
Equation 1:
| Zx = | VA2 | = | VA2 | Rref |
| I | VA1-VA2 |
Equipment List
- Tektronix AFG2021 arbitrary/function generator
- DPO4104 oscilloscope
- A 1 kΩ precision resistor
- Two Tektronix TPP1000 voltage probes
- A 10 uF ceramic capacitor
- An unknown capacito
How to Perform the Impedance Measurement
- Set up the test circuit as shown in Figure 2. Note that RESR and C are both associated with the ceramic capacitor under test,and that Rfg is the 50Ω output impedance of the function generator.
- Set the function generator to output a 1.9 V amplitude, 100 Hz sine wave.
- Adjust the vertical scale setting of the oscilloscope to use as much of the display as possible – by using as much of the range as possible, you will improve the accuracy of your voltage measurements.
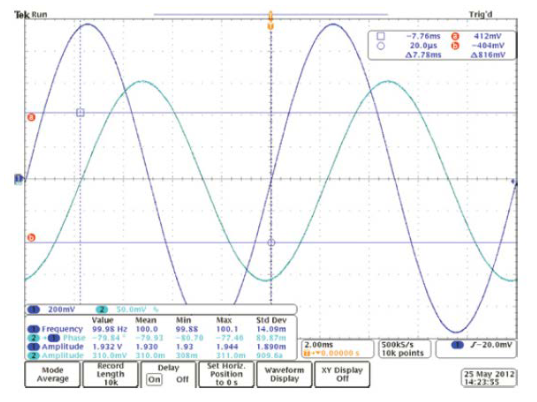
- Use the oscilloscope to probe at nodes A1 and A2. Figure 4 shows an example of the resulting waveform.
- Select the oscilloscope's average acquisition mode and set the number of averages to 128. This will reduce the effects of random noise on your measurements.
- Set the oscilloscope to measure the four parameters listed below. (An example is given in Figure 4.) a. Channel 1 frequency b. Phase between channel 2 and channel 1
- Carefully record both the four measurements.
- Replace the 10 µF capacitor with the unknown capacitor.
- Repeat steps 3 through 6 for the unknown capacitor.
c. Channel 1 amplitude
d. Channel 2 amplitude, as shown in Figure 4.
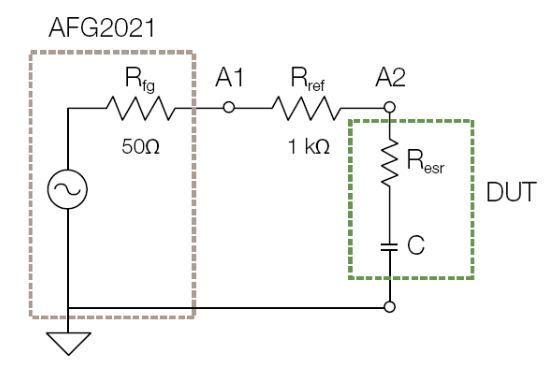
How to Calculate Impedance from Your Measurements
From the measurement setup, we know:
Stimulus frequency, f = 100 Hz
Precision Resistor, R1 = 1 kΩ
From the measurements taken on the oscilloscope and shown in Figure 3:
Voltage amplitude measured at A1, VA1 = 1.929 V
Voltage amplitude measured at A2, VA2 = 0.310 V
Phase difference between voltage measured at A2 relative to A1, 𝜃 = -79.95°
Note that at node A1, the voltage has a phase angle of 0°, that is it is in phase with the function generator output. At A2 the voltage is shifted ahead by the phase angle θ.
The impedance of the capacitor under test can be found using Equation 1, given above
The impedance can be expressed in polar form, where the magnitude is given by:
| Z = | VA2Rref |
| √V2A1-2VA1VA2cos𝜃+V2A2 |
The angle of the impedance is given by subtracting the two angles:
| ∝ = 𝜃 - tan-1 | -VA2 sin 𝜃 |
| VA1VA2 cos 𝜃 |
For the test in our example, we can use Equation 2 and Equation 3 to find the magnitude and angle of the impedance of the capacitor under test:
| Z = | (0.310)(1𝑥103) |
| √(1.929)2 - 2(1.929)(0.310) cos(-79.95°) + (0.310)2 |
| ∝ = 𝜃 - tan-1 | -0.310 sin(-79.95°) |
| 1.929 - 0.310 cos(-79.95°) |
| ∝ = | -89.197° |
Now we can convert to the rectangular form of the impedance to find the resistance and capacitance.
| Z = RESR - | j |
| 2𝜋𝑓C |
| Z = | Z cos ∝ + jZsin ∝ |
Using the equations above, we can solve for the ESR and Capacitance of the DUT:
| RESR = | Z cos ∝ |
| C = | -1 |
| 2𝜋𝑓Zsin ∝ |
Using Equation 4 and Equation 5 we can calculate the equivalent series resistance (ESR) and capacitance for the capacitor under test:
| RESR = | 163.193 cos(-89.197) |
| RESR = | 2.29 Ω |
| C = | -1 |
| 2𝜋(100)(163.193)sin(-89.197) |
| C = | 9.75 µF |
Analyzing and Interpreting Your Results
- Calculate the magnitude of the impedance, angle of the impedance, series resistance, and capacitance of the 10 uF capacitor. How do your results compare to the ones in the example calculations above. Show your calculation.
- Calculate the magnitude of the impedance, angle of the impedance, series resistance, and capacitance of the unknown capacitor.
- Compare the magnitude of the impedance, angle of the impedance, series resistance, and capacitance of the two capacitors. Explain why each parameter changed the way it did.
The right instruments are essential for accurate impedance measurements. Explore our range of oscilloscopes to find the perfect fit for your lab or project.
Unsure which oscilloscope is right for your specific impedance measurements? Our experts are here to help you choose with confidence.
Copyright © Tektronix. All rights reserved. Tektronix products are covered by U.S. and foreign patents, issued and pending. Information in this publication supersedes that in all previously published material. Specification and price change privileges reserved. TEKTRONIX and TEK are registered trademarks of Tektronix, Inc. All other trade names referenced are the service marks, trademarks or registered trademarks of their respective companies.
04/2013 48W-29165-0

