Introduction
Fourier analysis enables the conversion between signals in the time domain to signals in the frequency domain. Fast Fourier Transformation (FFT) computations are useful when acquiring DC signals such as current, voltage, and time and converting them into frequency and AC-based parameters such as current spectral density, 1/f noise, thermal noise, and AC impedance. Source measure instruments (SMUs) and the pulse measure unit (PMU) are modules for the 4200A-SCS Parameter Analyzer that measure and source current and voltage in the time domain. The time-based measurements on devices taken by these instruments can be converted into parameters in the frequency domain using FFT computations.
Beginning with the Clarius+ V1.9 software release, the 4200A-SCS Parameter Analyzer includes FFT analysis functions that enable the user to automatically make frequency-based calculations on time domain measurements without having to download the data and perform analysis in a separate tool. This enables the user to get important test results much faster. This application note explains these new functions along with some typical use cases for FFT parameter extractions including current spectral density measurements using both an SMU and the PMU, resistor thermal noise measurements, and AC impedance calculations of an RC circuit.
FFT Related Functions in the Clarius Formulator
The Clarius software has a built-in Formulator that enables the user to make data calculations on test data and on the results of other Formulator calculations. The Formulator provides a variety of computational functions, common mathematical operators, and common constants. Beginning with the Clarius V1.9 release, FFT formulas have been added to the Formulator. A screen capture of the Formulator with the FFT functions is shown in Figure 1.
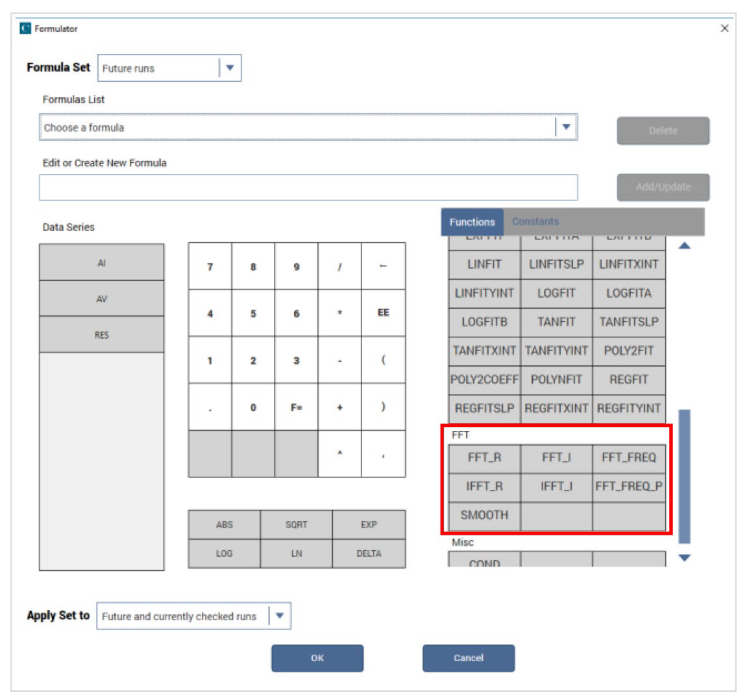
The built-in FFT functions and their descriptions are listed in Table 1. These equations can perform an FFT or an inverse FFT on real and imaginary input arrays and then output the real or imaginary components. Two of the formulas return an array of frequencies from an input time array. A smooth function uses digital filtering on an input array by zeroing out high frequency components.
| Formula | Description |
| FFT_R(Real, Imag) | Performs an FFT on the provided real and imaginary input arrays and then outputs the real components of the calculated FFT. |
| FFT_I(Real, Imag) | Performs an FFT on the provided real and imaginary input arrays and then outputs the imaginary components of the calculated FFT. |
| IFFT_R(Real, Imag) | Performs an inverse FFT on the provided input arrays and then returns the real parts scaled by 1/N where N is the number of samples. |
| IFFT_I(Real, Imag) | Performs an inverse FFT on the provided input arrays and then returns the imaginary parts scaled by 1/N where N is the number of samples. |
| FFT_FREQ(Time, Tolerance) | From an input time array, returns an array of frequencies that correspond to the frequencies of the FFT output |
| FFT_FREQ_P(Time, Tolerance) | From an input time array, returns an array of positive only frequencies that correspond to the frequencies of the FFT output |
| Smooth(X, Percent) | Performs digital filtering on an input array by zeroing out high frequency components. |
Table 1. FFT formulas and descriptions.
When using the FFT formulas, it’s best to take data in evenly-spaced time intervals. When converting a time array into an array of frequencies, the FFT_Freq function enables the user to enter a tolerance parameter to determine if the consecutively-spaced time data is evenly spaced. If the delta, expressed in percentage, between two points in the input time array is greater than the tolerance value, #REF will be returned to the Sheet.
The output size of the calculated real and imaginary data arrays will be a power of 2. As a result, the ideal number of acquired data points should be a power of 2 such as 64, 128, 256, 512, 1024, etc. If the number of data points is not a power of two, the returned number of points will be reduced so that they are a power of 2.
Example Tests Using FFT Equations
The Clarius Library contains several tests showing examples of using FFT formulas that convert time-based current or voltage measurements into frequency-dependent parameters. These examples include the SMU Current Spectral Density, Thermal Noise of a Resistor, PMU Current Spectral Density, and the AC Impedance of an RC circuit.
SMU Current Spectral Density vs Frequency Measurement
The SMU Current Spectral Density (smu-isd) test in the Clarius Library derives the current spectral density as a function of frequency from DC current measurements taken with an SMU as a function of time. Depending on the device and the application, this test may be able to be used to derive current noise from devices including 1/f noise.
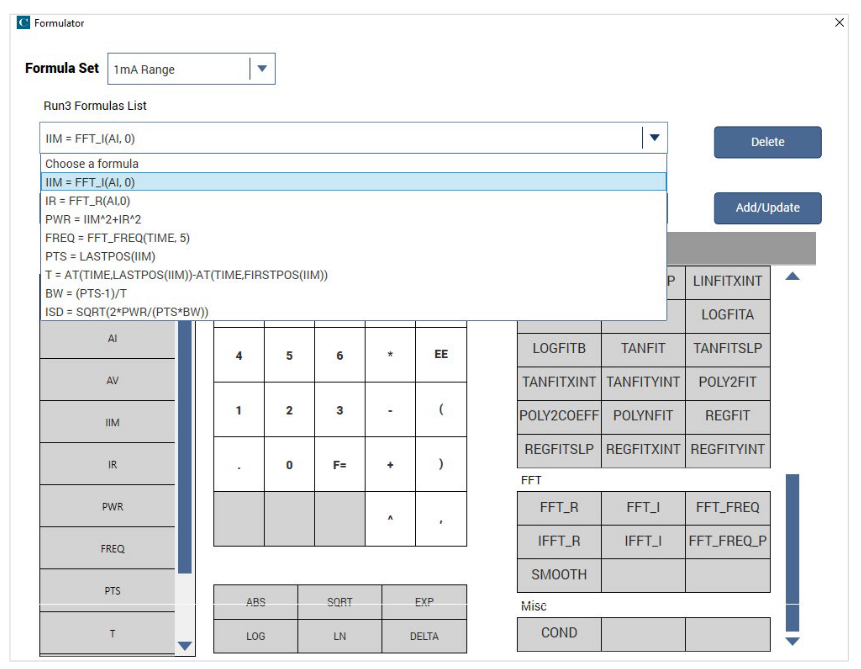
In this test, the DC current vs. time of the 4201-SMU is measured with an open circuit on three different current ranges (1 mA,1 µA, and 1 nA) using the Normal speed mode. Metal caps were placed on the Force HI and Sense HI terminals of the SMU.FFT equations to derive the real and imaginary components of the current, power, frequency, bandwidth, and current spectral density were calculated in the Formulator as shown in the screen capture shown in Figure 2.
The resulting current spectral density vs frequency curves of each of the three test Runs are shown in Figure 3. Because the current is measured with an open circuit, the noise floor of the SMU is basically what is derived. The frequency will change depending on the timing settings.
These graphs show the current noise spectral density, which is measured in A/sqrt(Hz), and not the noise of a single DC measurement, which is measured in amps. Expressed in terms of numerical Fast Fourier Transformation, the current spectral density is defined here as:
ISD = sqrt(2*PWR/(PTS*BW))
where:
PWR is the current amplitude squared, or PWR = Im(I)^2 + Re(i)^2
BW is the bandwidth of the time sampling
PTS is the number of points, which should be a power of 2
Bandwidth (BW) is defined as 1/dt, where dt is the time step between two measurements, assuming the time step between all measurements is a constant value.
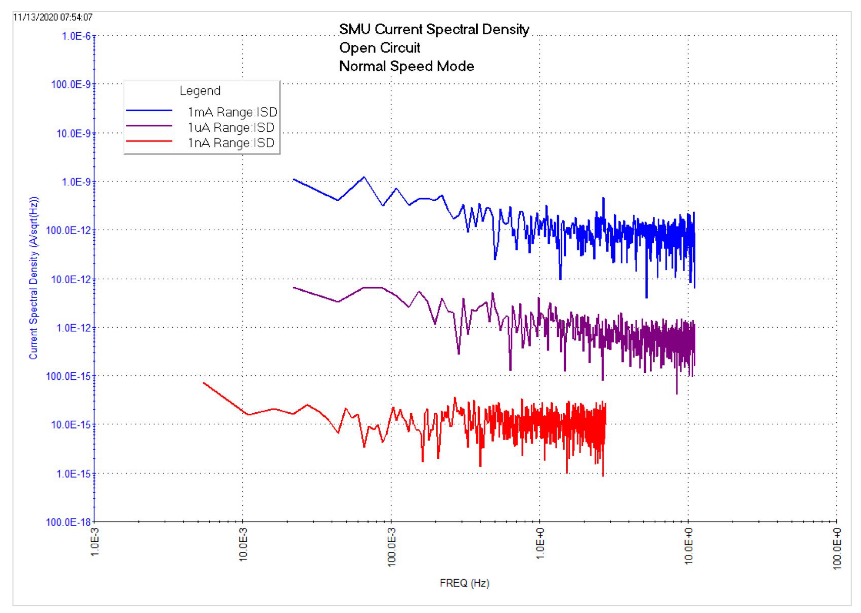
The measurement speed is controlled in the Test Settings Window. Even though the measurement time cannot be set directly, the measurement time, bandwidth and test frequencies are known and returned to the Sheet. When setting the speed modes, there is usually a trade-off between speed and noise of each single DC measurement. The faster the measurement speed is, the higher the noise will be. For measurements taken with a longer total test time, the bandwidth is smaller and therefore the noise is smaller.
The measurements in this test were taken on a fixed current range. Using a fixed measurement range, and not Auto Ranging, is important to keep the measurement time of each reading constant, which is needed for FFT calculations.
The sampling test mode is used because a constant bias is forced. In the mode, the number of readings must be entered.Even though a large number of readings are desirable when using FFT calculations, it’s not practical. In this test, 1024 readings were taken since 1024 is a power of 2. Table 2 lists the formulas used for the SMU Current Spectral Density Test.
| Formula | Description |
| IIM | Imaginary current array:IIM=FFT_I(AI,0) |
| IR | Real current array: IR=FFT_R(AI,0) |
| PWR | Power: PWR=IIM^2 + IR^2 |
| FREQ | Frequency array: FREQ=FFT_FREQ(TIME, 5) |
| PTS | Total number of points (of FFT calculated data): PTS=LASTPOS(IIM) |
| T | Total test time (of FFT calculated data): T=AT(TIME, LASTPOS(IIM))- AT(TIME,FIRSTPOS(IIM)) |
| BW | Bandwidth: BW=(PTS-1)/T |
| ISD | Current spectral density: ISD=SQRT(2*PWR/(PTS*BW)) |
Table 2. Formulas for the SMU Current Spectral Density Test.
Thermal Noise of a Resistor
Thermal, or Johnson, noise of a resistor can be calculated from DC voltage vs. time measurements on a resistor. The resistornoise test in the Test Library measures DC voltage at 0 A as a function of time and calculates the real and imaginary voltage arrays, power, frequency, bandwidth, and the voltage spectral density on a 1E9 ohm resistor. The resistor is placed between SMU1 and the GNDU. Once the test is executed, the thermal noise (VSD) is plotted as function of frequency and is shown in Figure 4.
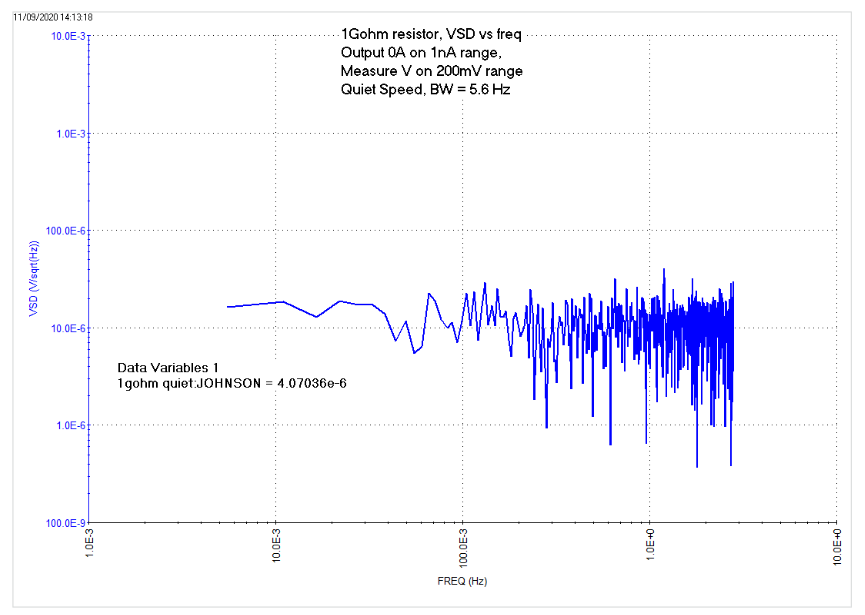
For this test, DC voltage measurements were made on the 200 mV range, and 0 A was forced on the 1 nA range. The noise current and Johnson noise of a 1E9 ohm resistor are also calculated. The theoretical thermal noise of a 1E9 ohm resistor is calculated to be about 4E-6 V rms using the equation: vn = sqrt(4*k*TEMP*1e9).
The actual equation for thermal power noise for a resistor is:
P = 4 * k * TEMP * BW
where:
k is Boltzmann’s constant, 1.38 E-23 J/K
TEMP is the environmental temperature (K)
BW is the bandwidth (Hz)
| Formula | Description |
| DELTAT | Time per reading: DELTAT=DELTA(TIME) |
| VR | Real voltage array: VR=FFT_R(AV,0) |
| VIM | Imaginary voltage array: VIM=FFT_I(AV,0) |
| PWR | Power: PWR=VR^2 + VIM^2 |
| FREQ | Frequency array: FREQ=FFT_FREQ(TIME, 5) |
| PTS | Total number of points: PTS=LASTPOS(VR) |
| JOHNSON | Thermal noise for 1E9 resistor: SQRT(4*K*300*1E9) |
| T | Total test time: T=AT(TIME, LASTPOS(VR))-AT(TIME,FIRSTPOS(VR)) |
| BW | Bandwidth: BW=(PTS-1)/T |
| VSD | Voltage spectral density: VSD=SQRT(2*PWR/(PTS*BW)) |
| IRMS | Current noise (for 1E9 resistor) IRMS=VSD/1E9 |
Table 3. Formulas for the Resistor Thermal Noise Test.
Formulas with descriptions for the resistor-noise test are listed in Table 3. Information on timing, range, number of points and other settings are similar to those discussed for deriving the SMU Current Spectral Density.
Acquiring Current Spectral Density of the PMU
Just like the SMU, the current spectral density of the 4225-PMU can also be derived from current and time measurements and FFT calculations. A test, pmu-isd, that calculates the PMU current spectral density with an open circuit on both the 100 µA and 100 nA ranges can be found in the Test Library. This test was generated by using the PMU_sampleRate user module in the PMU_freq_time_ulib user library. With this PMU test, the user can input a voltage bias for both CH1 and CH2, select a current range for CH2, and specify the total test time and the sample rate. A screen capture of the Configure view of the pmu-isd test is shown in Figure 5.
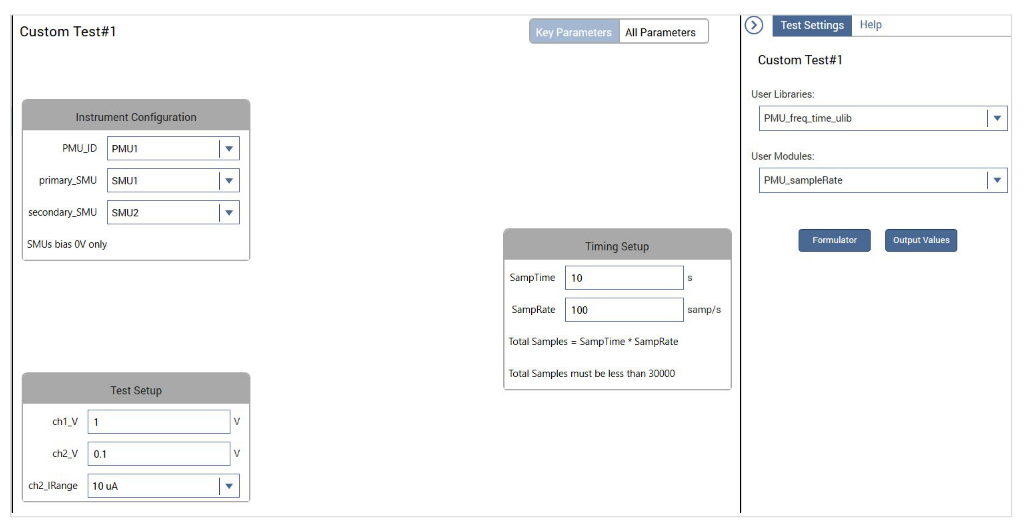
Like the SMU Current Spectral Density Test, the Formulator has several equations to derive the bandwidth, real and imaginary components of the test current, power, frequency, and the current spectral density. A screen capture of the derived graphs of the current spectral density vs. frequency on the 100 µA and 100 nA ranges is shown in Figure 6. Because the data was taken with an open circuit, these are measurements of the noise floor of the PMU on a fixed current range taken at a selectable sample rate.
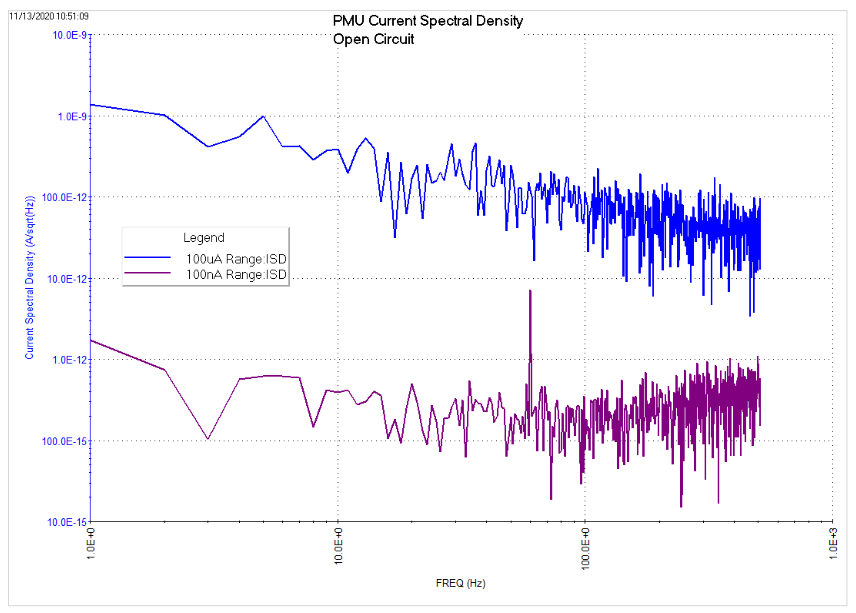
In the Configure view, the user inputs the total test time and the sampling rate. The number of points is equal to the total test time times the sampling rate. Choose input parameters so that the total number of points is a power of 2 since FFT computations will be performed on the data. For best results, a minimum of 20 points or more should be used. For this test, the bandwidth was 1024 Hz.
| Formula | Description |
| IIM | Imaginary current array on CH2: IIM=FFT_I(MEASI_CH2,0) |
| IR | Real current array on CH2: IR=FFT_R(MEASI_CH2,0) |
| PWR | Power: PWR=IIM^2 + IR^2 |
| FREQ | Frequency array: FREQ=FFT_FREQ(TIMEOUTPUT, 20) |
| PTS | Total number of points (on FFT calculated data): PTS=LASTPOS(IIM) |
| T | Total test time (on FFT calculated data): T=AT(TIMEOUTPUT, LASTPOS(IIM))- AT(TIMEOUTPUT, FIRSTPOS(IIM)) |
| BW | Bandwidth: BW=(PTS-1)/T |
| ISD | Current spectral density: ISD=SQRT(2*PWR/(PTS*BW)) |
Table 4. Formulas for the PMU Spectral Density Test.
Determining the AC Impedance of an RC Series Circuit
Using the two-channel 4225-PMU combined with the built-in FFT formulas enables the user to extract the AC impedance parameters of RC circuits. The PMU measures the current and voltage in the time domain, and the FFT computations in the Clarius Formulator convert these signals into parameters in the frequency domain.
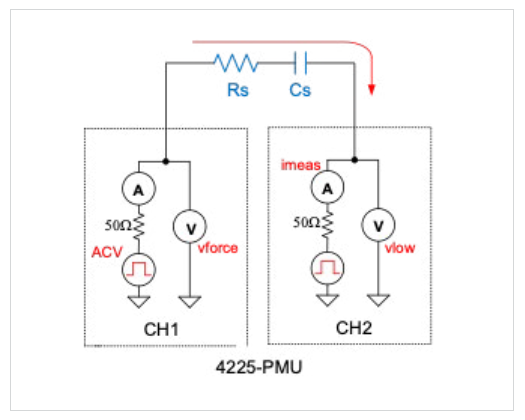
For example, a series RC circuit can be connected between CH1 and CH2 of the PMU as shown in Figure 7. CH1 outputs a periodic pulse waveform (ACV), and CH2 measures the resulting current (imeas). From the measured current, voltage, and time, the AC impedance parameters of the test circuit, such as the series resistance (Rs) and reactance (Xs), the real and imaginary parts of the impedance, are derived using FFT computations. The capacitance (Cs) and dissipation factor (D) can be derived using Rs and Xs.
A test, R-C Circuit AC Impedance Calculations (rs-cs-ac-impedance), that extracts AC parameters of a series RC circuit has been added to the Test Library. In this example test, CH1 of the PMU outputs a pulsed waveform with a specified amplitude and test frequency. The number of cycles and number of points per period are also specified. Calculations are configured in the Formulator to extract the AC impedance parameters of a 100 kohm, 10 nF series R-C circuit. A screen capture of the Configure view of this test is shown in Figure 8.
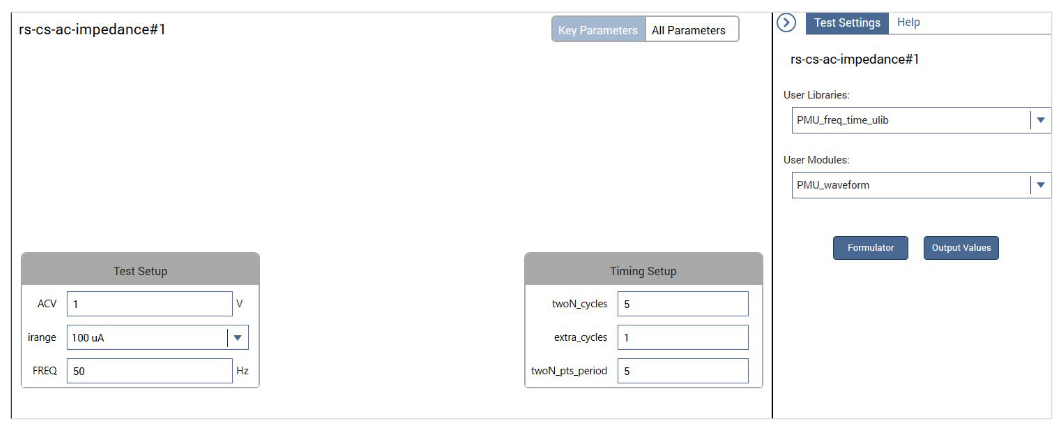
For this test, the voltage pulse magnitude of CH1 (ACV), the current measurement range of CH2 (irange), test frequency (FREQ), n number of 2^n cycles, and n number of 2^n points per period are entered into the Configure view. Table 5 lists the input parameters for this test. Based on these input parameters, the PMU builds a voltage segment waveform with current measurements.
| Name | Values | Description |
| ACV | 0.02V to 5V (0.1V default) | Magnitude of voltage pulses from CH1 |
| irange | All current ranges (for 10V range) | Current measurement range of CH2 |
| FREQ | 1e-2 to 1e3 | Test frequency |
| twoN_cycles | N = 3 to 6 (default 5) | 2^n number of cycles |
| extra_cycles | 1-5 | Additional cycles that occur before the actual test to exclude data transients and to allow for measurements to settle. These measurements are not returned to the Sheet. |
| twoN_pts_ period | N = 3 to 6 (default 5) | 2^n points per period |
Table 5. Input parameters of rs-cs-ac-impedance Test.
A large number of cycles is usually desirable when performing FFT computations on periodic signals, however,acquiring a lot of data isn’t usually practical. For sufficient accuracy try using at least 32 (2^5) cycles with 32 (2^5) data points per cycle. In the rs-cs-ac-impedance Test, both the number of cycles and the points per period are 32.
If you want to extract both the series resistance (Rs) and capacitance (Cs), its best to choose a test frequency that is approximately: F = 1/RC. However, this may take some experimenting. Usually there is a trade-off between the measurement of capacitance or resistance. More accurate measurement of capacitance requires a smaller D, <0.1, and more accurate measurements of resistance requires a higher D values, D>1. Selection of F=1/RC provides a trade-off scenario when you have adequate accuracy to extract both Rs and Cs.
Once the test is executed, the number of points that are returned to the Sheet equal can be calculated by the following equation:
Total number of points per test = number of cycles × number of points per cycle
For this test, the total number of points = 32 x 32 = 1024. Arrays of the measured voltages of the pulses (vforce) on CH1, the voltage of CH2 (vlow), time, and the measured current on CH2 (imeas) are returned to the Sheet. Descriptions of the output parameters are listed in Table 6.
| Name | Description |
| vforce | Array of measured voltages (CH1) |
| vlow | Array of measured voltages (CH2) |
| time | Array of time measurements |
| imeas | Array of resulting current (CH2) |
| usedFreq | Test frequency |
Table 6. Output parameters of rs-cs-ac-impedance Test.
From the returned values, many AC parameters can be extracted. For this test, all the calculated parameters for the RC series circuit appear in Table 7, which lists the formula names and descriptions.
| Formula Name | Description |
| IREAL | The real part of the FFT of the measured current: IREAL = FFT_R(IMEAS, 0) |
| IIMAG | The imaginary part of the FFT of the measured current: IIMAG = FFT_I(IMEAS, 0) |
| VREAL | The real part of the FFT of the forced voltage: VREAL = FFT_R(VFORCE, 0) |
| VIMG | The imaginary part of the FFT of the forced voltage: VIMG = FFT_I(VFORCE,0) |
| FREQS | The array of frequencies calculated from the time array: FREQS = FFT_FREQ(TIME, 20) |
| VPW | The array of the square of the amplitude of the FFT voltage VPW = (VREAL^2 +VIMG^2) |
| MAXPS | Position of the main voltage harmonic MAXPS = MAXPOS(VPW) |
| IPWR | The array of the square of the amplitude of the FFT current IPWR = (IREAL^2 +IIMAG^2) |
| RS | Series Resistance: RS = -(VREAL*IREAL+VIMG*IIMAG)/IPWR |
| XS | Reactance: XS = -(VIMG*IREAL-VREAL*IIMAG)/IPWR |
| D | Dissipation factor: D = RS/XS |
| CS | Series capacitance CS = -1/ (6.28 *XS * FREQS) |
| CS_AT_FRQ | Series capacitance at main harmonic frequency CS_AT_FRQ = AT(CS, MAXPS) |
| RS_AT_FRQ | Series resistance at main harmonic frequency RS_AT_FRQ = AT(RS, MAXPS) |
| D_AT_FRQ | Dissipation factor at main harmonic frequency D_AT_FRQ = AT(D, MAXPS) |
Table 7. Calculated parameters.
All the output and calculated parameters also are returned to the Sheet and graphed in the Analyze view as shown in Figure 9. The data can be plotted in both the time domain and the frequency domain. In Graph 1 the voltage and current waveforms are plotted as a function of time. In Graph 2, the array of the squares of the amplitudes of the voltage (VPWR) and current (IPWR), are graphed as a function of the frequency. Cs, Rs, and D at the main harmonic frequency are derived and appear in the last three columns of the Sheet.
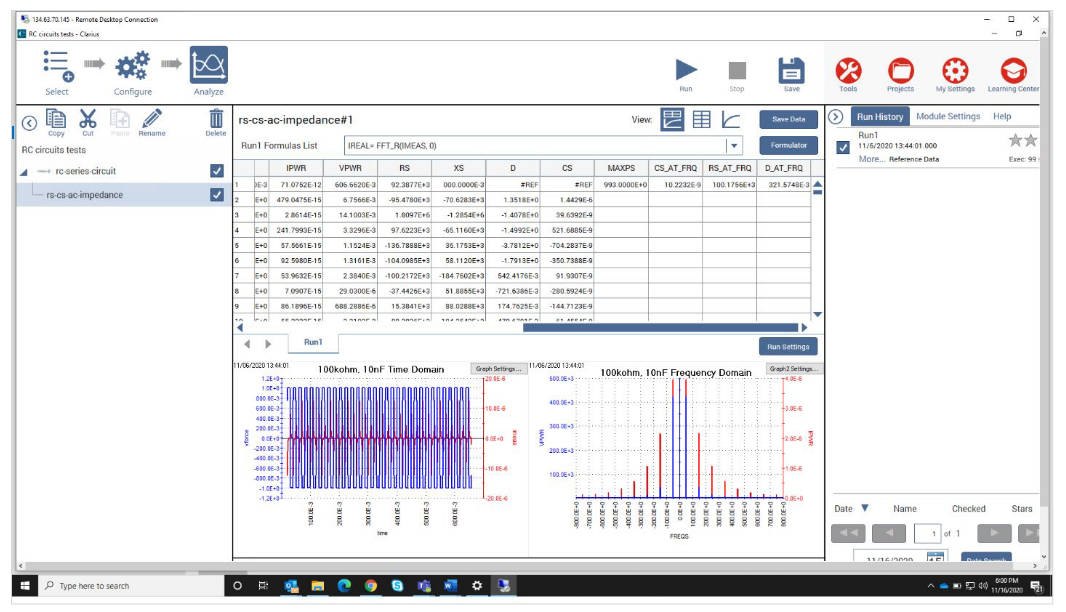
The rs-cs-ac-impedance Test uses the PMU_waveform user module in the PMU_freq_time_ulib user library. This user module can also be used for performing other tests that require a pulsed waveform at a specific test frequency.
Conclusion
The ability to perform FFT computations on DC current and voltage measurements in the 4200A-SCS Parameter Analyzer enables many AC parameter extractions, including current spectral density, thermal noise, and AC impedance. This enables the user to get test results much faster since a separate tool is no longer required to perform FFT analysis.
Find more valuable resources at TEK.COM
Copyright © Tektronix. All rights reserved. Tektronix products are covered by U.S. and foreign patents, issued and pending. Information in this publication supersedes that in all previously published material. Specification and price change privileges reserved. TEKTRONIX and TEK are registered trademarks of Tektronix, Inc. All other trade names referenced are the service marks, trademarks or registered trademarks of their respective companies.
112420 1KW-73767-0

