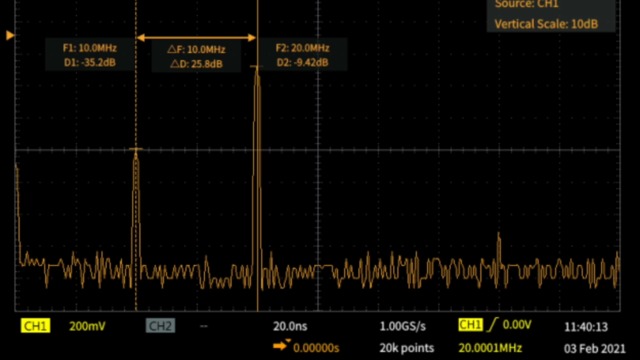
質問:
オシロスコープのFFT機能とは?
回答:
オシロスコープのFFT(高速フーリエ変換)演算機能は、時間領域の信号を周波数領域の表現に変換するために使用されます。この機能により、ユーザーは信号の周波数成分を表示・分析することができ、時間領域では見えない可能性のある信号品質や動作に関する重要な詳細を明らかにすることができます。FFTを使用することで、ユーザーは信号内の特定の周波数、高調波、ノイズを識別し、より効果的に問題のトラブル・シューティングと診断を行うことができます。一般的な応用例は以下の通りです。
- 電力線の高調波分析
- システムの高調波含有量と歪みの測定
- DC電源のノイズ特性評価
- フィルタやシステムのインパルス応答テスト
- 振動信号の分析
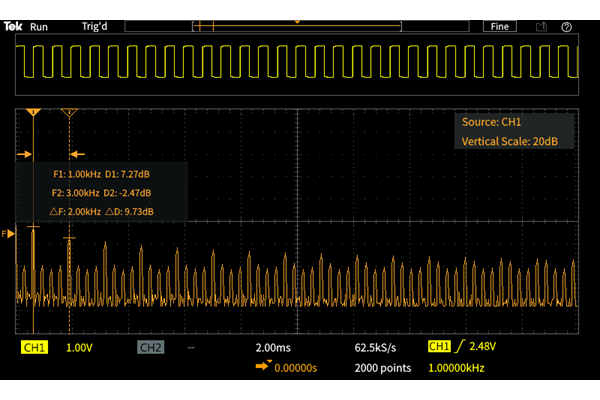
TBS1000CでのFFT表示例
FFT(高速フーリエ変換)とは?
FFT(高速フーリエ変換)とは、信号処理、データ分析、画像処理など様々な分野で使用される基本的な数学的手法です。これは時間領域のデータを周波数領域の表現に変換する強力なアルゴリズムであり、信号やデータセットの周波数成分を分析することを可能にします。このセクションでは、FFTとは何か、どのように機能するのか、そしてその応用について詳しく説明します。
FFTの基礎
FFTは時間領域のデータを周波数領域の情報に変換するための基本的なツールであり、エンジニアや科学者が信号のスペクトル内容を分析することを可能にします。FFTの核心は、時間領域でサンプリングされたデジタル信号をその周波数成分に分解する能力にあります。この変換により、信号の基本となる正弦波の周波数と振幅が明らかになり、そのスペクトル特性への洞察が得られます。信号の周波数内容を理解することで、エンジニアは信号の主要な特徴、ノイズ、歪みを識別して分離することができます。DFT(離散フーリエ変換)と比較すると、FFTはより高速で、リアルタイム・アプリケーションや大規模データセットに実用的です。
サンプリング・レート、ブロック長、周波数分解能
FFTの有効性に影響を与える2つの重要な要素は、サンプリング・レートとブロック長(または分析されるデータポイント数)です。
- サンプリング・レート:サンプリング・レートは、正確に測定できる周波数の範囲を決定します。ナイキストの定理によると、サンプリング・レートは対象とする最高周波数の少なくとも2倍でなければなりません。この条件が満たされない場合、エイリアシングが発生し、高周波成分が低周波スペクトルに誤って折り返され、結果が歪みます。
- ブロック長と周波数分解能:ブロック長はFFTの周波数分解能に直接影響します。ブロック長が大きいほど、より細かい分解能が可能になり、近接した周波数をより良く区別できます。ただし、特にリアルタイム・アプリケーションでは、ブロック長が大きいほど計算能力と時間がより多く必要になる場合があります。
ナイキスト周波数とエイリアシング
ナイキスト周波数は、サンプリング・レートの半分に等しく、FFT分析で正確に捉えることができる最高周波数を表します。信号にナイキスト周波数よりも高い成分が含まれている場合、エイリアシングが発生します。エイリアシングは、サンプリング・レートを上げるか、サンプリング前に高周波成分を除去するためのアンチエイリアシング・フィルターを使用することで軽減できます。
FFTのアルゴリズム効率
FFTの効率性は、正弦波関数の対称性を利用することから生まれ、標準的なDFTと比較して計算負荷を大幅に削減します。この効率性により、通信、信号処理、制御システムなど、迅速なリアルタイム・データ処理を必要とするアプリケーションに理想的です。
精度向上のための窓関数処理と平均化技術
多くの実際のアプリケーションでは、信号はFFTの周波数ビンと完全に一致しません。このミスアライメントはスペクトル漏れを引き起こし、ある周波数からのエネルギーが隣接するビンにこぼれ出します。これに対抗するため、窓関数処理技術が適用され、データにハミング、ハニング、ブラックマン・ハリスなどの窓関数を乗算することで漏れを減少させ、周波数表現の精度を向上させます。
さらに、平均化技術を使用して、周波数領域での非周期的または雑音の多い信号の明瞭さを向上させることができます。複数のFFT結果を平均化することで、ランダムなノイズが減少し、信号の真のスペクトル内容が明らかになります。
FFTの用途
1.信号処理
- 音声分析: FFTは音声信号の分析と操作のために音声処理で使用されます。音声圧縮、イコライゼーション、ピッチ検出などのタスクに不可欠です。
- 画像処理: 画像処理では、FFTは画像のフィルタリング、圧縮、特徴抽出などのタスクに使用されます。
2.通信システム
- 無線通信: FFTは、Wi-Fiや携帯電話ネットワークなどの無線通信システムにおいて、信号の変調と復調に重要な役割を果たします。
- スペクトル分析: 利用可能な帯域幅を効率的に活用するために、通信信号の周波数スペクトルを分析するのに使用されます。
3.科学研究
- 物理学: FFTは物理学の様々な分野で実験データを分析するために使用されます。X線結晶学、核磁気共鳴(NMR)分光法、重力波検出などがあります。
- 天文学: 天文学者は天体や現象を研究するために、望遠鏡や電波望遠鏡からのデータを処理・分析するためにFFTを使用します。
4.データ分析
- 時系列分析: FFTは、株式市場のトレンドや気候データなど、データの周期的なパターンやトレンドを識別するための時系列分析に有用です。
- 振動分析: 機械・構造工学では、FFTは振動を分析し、機械の潜在的な問題を検出するために使用されます。
FFTに関する資料
結論
要約すると、FFTは、時間領域のデータを周波数領域の表現に変換するために使用される多用途で強力な数学的アルゴリズムです。その効率性と幅広い用途により、信号処理や通信システムから科学研究やデータ分析まで、さまざまな分野で重要なツールとなっています。FFTを理解することで、研究者やエンジニアはデータの基本的な周波数成分について貴重な洞察を得ることができ、幅広い応用において深い理解とより良い意思決定を促進します。
FAQの該当製品:
製品シリーズ: デジタル・ストレージ・オシロスコープ|TBS1000Cシリーズ TBS2000Bシリーズ・デジタル・オシロスコープ 2シリーズMSOポータブル・ミックスド・シグナル・オシロスコープ 3シリーズMDOミックスド・ドメイン・オシロスコープ
製品:
FAQ ID 62251
すべてのFAQを表示 »