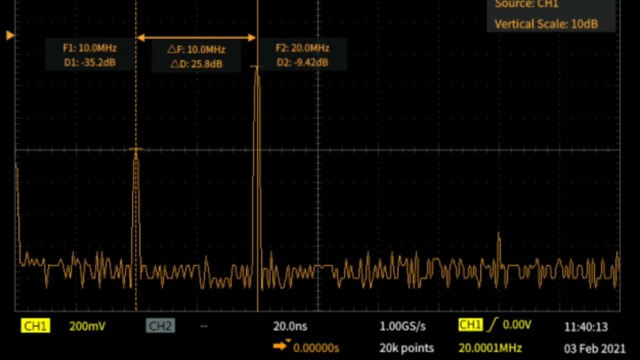
問題:
What is FFT (Fast Fourier Transform) math function of an oscilloscope used for?
答案:
The FFT (Fast Fourier Transform) math function on an oscilloscope is used to convert a time-domain signal into its frequency-domain representation. This allows the user to view and analyze the frequency components of the signal, which can reveal important details about signal quality and behavior that may not be visible in the time domain. By using FFT, users can identify specific frequencies, harmonics, or noise within a signal, helping them troubleshoot and diagnose issues more effectively. Common applications include:
- Analyze harmonics in power lines
- Measure harmonic content and distortion in systems
- Characterize noise in DC power supplies
- Test impulse response of filters and systems
- Analyze vibration signals
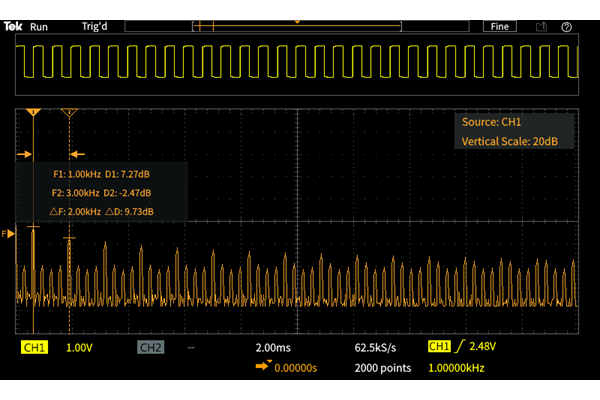
Screenshot example of FFT on TBS1000C
What is Fast Fourier Transform (FFT)?
The Fast Fourier Transform, commonly known as FFT, is a fundamental mathematical technique used in various fields, including signal processing, data analysis, and image processing. It is a powerful algorithm for transforming time-domain data into its frequency-domain representation, enabling us to analyze the frequency components of a signal or data set. In this section, we will delve into the details of what FFT is, how it works, and its applications.
Understanding FFT - Time-Domain to Frequency-Domain Transformation
The Fast Fourier Transform (FFT) is a fundamental tool for converting time-domain data into frequency-domain information, allowing engineers and scientists to analyze the spectral content of signals. At the core of FFT is its ability to decompose a digital signal—sampled in the time domain—into its frequency components. This transformation reveals the signal's underlying sinusoidal frequencies and amplitudes, offering insight into its spectral characteristics. By understanding the frequency content of a signal, engineers can identify and isolate key signal features, noise, and distortions. Its efficiency compared to the Discrete Fourier Transform (DFT) makes it practical for real-time applications and large datasets.
Sampling Rate, Block Length, and Frequency Resolution
Two key factors impact the effectiveness of FFT: the sampling rate and the block length (or the number of data points analyzed).
- Sampling Rate: The sampling rate determines the range of frequencies that can be accurately measured. According to the Nyquist Theorem, the sampling rate must be at least twice the highest frequency of interest. If this condition is not met, aliasing occurs, where high-frequency components are incorrectly folded back into the lower frequency spectrum, distorting the results.
- Block Length and Frequency Resolution: The block length directly affects the frequency resolution of the FFT. A larger block length enables finer resolution, allowing for better distinction between closely spaced frequencies. However, larger block lengths may require more computational power and time, especially for real-time applications.
The Nyquist Frequency and Aliasing
The Nyquist frequency, equal to half of the sampling rate, represents the highest frequency that can be accurately captured in an FFT analysis. If signals contain components higher than the Nyquist frequency, aliasing will occur. Aliasing can be mitigated by increasing the sampling rate or using anti-aliasing filters to remove high-frequency components before sampling.
Algorithmic Efficiency of FFT
The efficiency of FFT stems from its use of symmetry in sinusoidal functions, significantly reducing the computational burden compared to a standard DFT. This efficiency makes FFT ideal for applications that require rapid, real-time data processing, such as telecommunications, signal processing, and control systems.
Windowing and Averaging Techniques for Improved Accuracy
In many real-world applications, signals do not perfectly align with the frequency bins of the FFT. This misalignment leads to spectral leakage, where energy from one frequency spills into adjacent bins. To counter this, windowing techniques are applied, multiplying the data by a window function (such as Hamming, Hanning, or Blackman-Harris) to reduce leakage and improve the accuracy of frequency representation.
Additionally, averaging techniques can be used to enhance the clarity of non-periodic or noisy signals in the frequency domain. By averaging multiple FFT results, random noise is reduced, revealing the true spectral content of the signal.
Applications of FFT
1. Signal Processing
- Audio Analysis: FFT is used in audio processing to analyze and manipulate audio signals. It's essential in tasks like audio compression, equalization, and pitch detection.
- Image Processing: In image processing, FFT is employed for tasks such as image filtering, compression, and feature extraction.
2. Communication Systems
- Wireless Communication: FFT plays a critical role in modulating and demodulating signals in wireless communication systems like Wi-Fi and cellular networks.
- Spectrum Analysis: It's used to analyze the frequency spectrum of communication signals to ensure efficient utilization of the available bandwidth.
3. Scientific Research
- Physics: FFT is used in various branches of physics to analyze experimental data, such as X-ray crystallography, nuclear magnetic resonance (NMR) spectroscopy, and gravitational wave detection.
- Astronomy: Astronomers use FFT for processing and analyzing data from telescopes and radio telescopes to study celestial objects and phenomena.
4. Data Analysis
- Time Series Analysis: FFT is valuable in time series analysis for identifying periodic patterns and trends in data, such as stock market trends or climate data.
- Vibration Analysis: In mechanical and structural engineering, FFT is employed to analyze vibrations and detect potential issues in machinery.
Resources Related to FFT
- FFT Applications for TDS Oscilloscopes
- VIDEO: How to Set Up an FFT on an Oscilloscope
- Get More from Your Basic Oscilloscope with the FFT Function
Conclusion
In summary, Fast Fourier Transform (FFT) is a versatile and powerful mathematical algorithm used for transforming time-domain data into its frequency-domain representation. Its efficiency and widespread applications make it a crucial tool in various fields, from signal processing and communication systems to scientific research and data analysis. Understanding FFT allows researchers and engineers to gain valuable insights into the underlying frequency components of data, facilitating a deeper understanding and better decision-making in a wide range of applications.
常見問答集 ID 62251
檢視所有常見問答集 »