タイミング・ジッタの分析と評価
タイミング・ジッタ(または単に「ジッタ」)は、電圧の遷移でタイミング情報を表すあらゆる電気システムにとって付き物の好ましくない現象です。従来、 電気システムに比較的遅い信号レートを採用して、タイミング・ ジッタの悪影響を軽減していました。そ の結果、ジッタに誘発されるエラーは、そのエラーにより破損さ れるタイム・インターバルと比較すると小さなものでした。今日 の高速シリアル・バスやデータ・リンクに伴うタイミング・マージン は、システム設計において、より厳格にジッタをコントロールす る必要があることを示しています。
信号レートが2GHzに上昇し、節電のために電圧振幅が小さくなる に伴い、システムにおけるタイミング・ジッタは信号インターバ ルの大部分を占めるようになっています。こうした環境では、ジッ タは基本性能を制限するようになります。ジッタとは何か、ジッ タをどのように評価するかを理解することは、高い信頼性で性能 要件を満たす高速システムをうまく採用するための第一歩です。
詳細な定義については第2章で取り上げますが、理論的には、ジッ タはタイミング・エッジの「正しい」位置からのずれです。タイミン グに基づくシステムでは、タイミング・ジッタは非理想性を示す 最も分かりやすく、直接的な形態です。ジッタはノイズの一種な ので、ランダム・プロセスとして処理され、統計的に評価されな ければなりません。
ジッタを統計的に測定する方法があれば、部品やシステムを互い に、また選択した限界まで比較できます。しかし、これだけでは 最新の設計を効率的にさらに改良・デバッグできません。ジッタ を完全に解析することによってのみ根本的な原因を特定し、試行 錯誤を繰り返すのではなく、系統的にジッタを減少させることが できます。この解析でジッタのビジュアル化と分析が行えますが、 これらについては第3章と第4章で説明します。
電気ジッタと光ジッタの原因、動作、評価には多くの類似点がありますが、光システムのジッタ測定で使用する機器は、電気システムの場合と異なります。本書では主に電気システムにおけるジッタについて説明します。
第1章:ジッタがもたらす問題
「推測するのに金はかからない。間違った推測をすると高くつく」中国のことわざ
なぜジッタを考慮する必要があるのか?ジッタはシステムの性能にどのような影響を及ぼすのか?本章では、高速コンピュータ・バスとシリアル・データ・リンクの2つの場合について検討します。それぞれの場合におけるジッタの影響を詳細に考察します。
コンピュータ・バス設計
たとえば、新しい組込み型プロセッサを設計していて、しかもフ ラッシュ・メモリの読込み時に時折データ・エラーが発生すると します。設計エンジニアは、フラッシュ・メモリのCE(チップ・ イネーブル)を生成するアドレス・デコードが、WE(ライト・イ ネーブル)の立上りエッジを基準にした必要なセットアップ時間 を満たしていないのではないかと考えます。高速オシロスコープ でCEおよびWEの信号をプロービングし、タイミングの関係を観 測します。単発アクイジションを10回して、87〜92nsの時間を 測定しますが、すべて最小限のセットアップ時間75nsを十分な マージンで上回っています。しかし、適切なマージンとは何でしょ うか?これらの時間は、要求されたセットアップ時間に違反して いるという懸念を晴らすのに十分なのでしょうか?発生すると考 えられる違反は、この時間の何パーセントでしょうか?
無限パーシスタンス・モードで数百万の波形を重ね書きして評価し、セットアップ時間がわずか82nsであることを観測した後、結局はセットアップ時間の問題かもしれないという結論を下します。しかし、この問題はシステムのクロック周期の変動、アドレス・デコーダ、あるいはどこか他の違反が原因なのでしょうか?
シリアル・データ・リンク
Gigabit Ethernet 物理層トランシーバ・チップの開発期限が繰り 上がり、まもなく外部の検査会社で行われるコンプライアンス・ テスト(認証試験)を心配しているとします。規格の仕様では、ロー カル・データ・クロック(再生クロック)に対するデータ・ジッ タ測定と、ジッタのない基準クロックに対するクロック・ジッタ 測定が要求されます。どんな状況でも、コンプライアンス試験で 部品が規格を満たすのに十分なマージンを備えていることを確認 する必要があります。
まず、無限パーシスタンス・モードでオシロスコープを使用して データ・クロックのピーク・トゥ・ピーク・ジッタを確認します。 このオシロスコープは画面上でヒストグラム・ボックスを定義で きるので、この機能を利用してエッジ位置のヒストグラムを作成 します。読み取ったピーク・トゥ・ピーク値は550psですが、仕 様ではこの値は300ps未満でなければなりません。ただし、 300psという仕様は5kHzのハイ・パス・フィルタでジッタをフィ ルタリングした後の値です。あいにく、ヒストグラムのジッタの どの部分が低い周波数によるもので、無視しても良いかを判断す る方法はありません。
次にクロックに対するデータ・ラインのジッタを観測します。こ れも仕様の制限に近付き過ぎています。しかし、このジッタは開 発したチップ内でなく、正確な設計方法に従わずに、差動データ・ ラインをレイアウトしたテスト・ボードから信号をピックアップ したためではないかと考えられます。テスト・ボードのスイッチン グ電源が原因の可能性はありましたが、測定されたジッタのどの 程度がこの原因によるものか判断する必要があります。
この場合と前述した場合は双方とも、高性能オシロスコープでさえ、すべての疑問に答えられないことがある例です。設計に絶対的な確信を得るには、さらに2つのツールが必要です。それは、高度なジッタ解析の手段とタイミング・ジッタの基本的な原因と特性を十分に理解することです。
第2章:ジッタ(jitter)とは?
この単純で直感的な定義は、SONET仕様1で以下のように規定されています。
「ジッタとは、デジタル信号の有意な瞬間の時間的な理想位置からの短期的な揺らぎと定義される」
これはジッタの本質をよく掴んでいますが、この定義を正しく使用する前に、いくつかの用語(短期的(ショートターム)、有意瞬間、理想位置)を明確にする必要があります。
実際のアプリケーションでは、ジッタにはランダムな成分がある ため、統計用語で表さなければいけません。平均値、標準偏差、 有効区間のクオリファイアなどのメトリックスを使用して、意味 のある再現性の高い測定を確立しなければなりません。以下に述 べる内容の基礎となる統計数学の基本的な考え方についての説明 は本書の目的ではありませんが、巻末の参考文献はさらに深く掘 り下げる場合に役立ちます。
2.1 ショートターム・ジッタとワンダの定義
タイミング変動は、一般に“変動”対“時間”のフーリエ解析に 基づいて、ジッタとワンダの2種類に分類されます(第3章の3.3 〜3.4で、この種の解析について詳述します)。ゆっくり発生する タイミング変動をワンダと言います。ジッタはそれより速く発生 するタイミング変動です。ワンダとジッタの間のスレッショルド は、ITU2によれば10Hzですが、他の定義もあるかもしれません。 多くの場合、ワンダはクロック・リカバリ回路により効果的に除 去されるため、シリアル通信リンクに対してほとんど影響を与え ません。
2.2 有意瞬間の定義: 基準レベル
ここで定義する有意瞬間は、デジタル信号のロジック・ステート 間のトランジション、つまりエッジのことです。具体的に言うと、 有意瞬間とは遷移する信号が選択された振幅スレッショルドを横 切るその時点です。この振幅スレッショルドは、基準レベルまた は決定スレッショルドと言われることもあります。2レベル信号(最 も一般的な場合)では、平均信号電圧はこの基準レベルとしてよ く使用されます。対象の信号をシュミット・トリガ入力で受ける 場合、立上りエッジの解析には基準レベルの1つを使用し、立下り エッジの解析には別の基準レベルを使用するのが望ましいでしょ う。
高速信号では、トランジションは立上り時間とスルー・レートに 制限を受けるアナログ・現象なので、本書の定義では、デジタル 信号ということばはおそらく楽観的かもしれません。信号が基準 レベルを横切って増減している短いけれど、有限の時間では、波 形を歪ませる電圧ノイズは比例的にタイミング・ジッタを増加さ せます。
2.3 理想位置の定義:クロック・リカバリ
デジタル信号の理想位置からのずれを測定する前に、理想位置を 特定しなければなりません。クロック信号のように0と1が交互に 続く信号の場合、理想位置は理論的には測定する信号と同じ平均 周波数と位相を持つジッタのないクロックと一致します。データ 信号を使用する場合は一層注意しなければいけません。それは列 になって同じビットが2つ以上続くと、イベント(トランジション) が発生しないからです。クロック・リカバリとは、基準クロック のタイミングを確立するプロセスを言います。
クロック・リカバリの1つの方法は、最小2乗法という意味からも測定するイベントに最適な一定周波数のクロックを使用することです。これは、以下の式で示す基準クロックを前提とすることを示しています。
Α . sin(ωct + φc)
ただし、ωcとφcは定数です。定数は、基準クロックと測定する クロックとの間の時間誤差を2乗した合計が最小になるように選択 します。これは、連続するデータの有限長ブロックを解析する場 合には、優れたアプローチです。データの長さが十分に長い場合、 そのジッタ測定にはジッタだけでなく、ワンダも含まれることが あります。この場合、その後にハイ・パス・フィルタを使用して、ワン ダ成分を取り除くことができます。
クロック・リカバリのもう1つの効果的な方法は、PLL(Phase Locked Loop)を使用することです。PLLは、測定するデータの シンボル・レートで生じるゆっくりした変動に常に追従するため、 信号に残留するジッタに対してハイ・パス・フィルタとして機能 します。ほとんどのデータ通信リンクではレシーバにPLLを使用 しているので、この測定アプローチには、測定するデバイスが使 用されているシステムの動作をモデル化できる利点があります。
一貫性と再現性のある測定を行うために、多くのデータ通信仕様 では「Golden PLL」が定められています。この場合のGoldenと はPLLの特性が正確に定義され、厳格にコントロールされている ことを意味します。これらの仕様に準拠するPLLを使用して、複 数のデバイスのジッタを測定する場合、ジッタを客観的に比較し、 そのデバイスが使用されているシステムを論理的に関連付けるこ とができます。
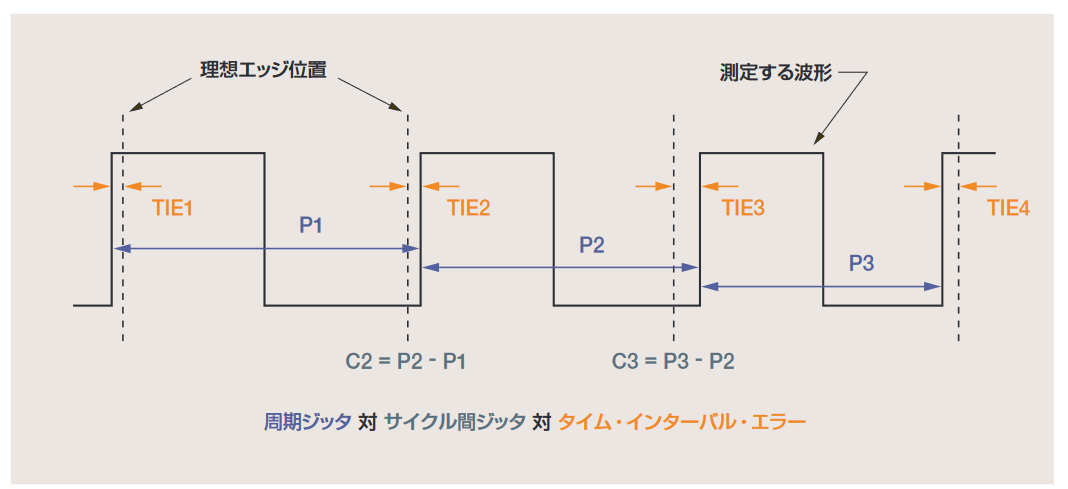
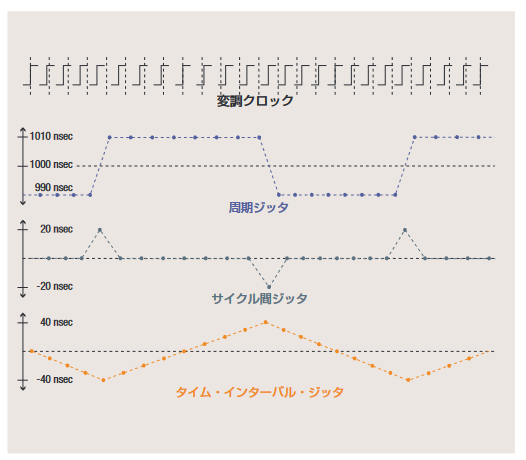
2.4 周期ジッタ、サイクル間ジッタ、そして TIE
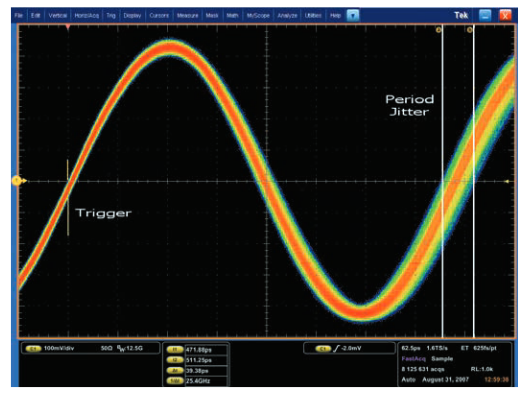
1つの波形上でジッタを測定する方法には、周期ジッタ、サイクル 間ジッタ、タイム・インターバル・エラー(TIE)などいくつかあ ります。これらの測定が互いにどのように関連しているか、何を 明らかにするかを理解することが重要です。図2.4aは、タイミン グ・ジッタを持つクロック信号を示しています。点線はクロック にジッタのない場合の理想的なエッジ位置を示します。
測定P1、P2、P3で示されている周期ジッタは、単に波形の各ク ロック・サイクルの周期を測定するだけです。これは、最も簡単 で直接的な測定です。そのピーク・トゥ・ピーク値は、オシロスコー プの表示モードを無限パーシスタンスに設定し、画面上にクロッ クが1周期以上表示されるように調整して観測できます。オシロ スコープが最初のエッジでトリガをかける場合、周期ジッタは2番 目のエッジで観測できます。これは図2.4bに示されています。
図2.4aのC2、C3に示されているサイクル間ジッタは、クロッ ク周期が2つの隣接するサイクル間でどのくらい変化するか測定 します。図に示されているように、サイクル間ジッタは、周期ジッ タに1次差分(微分)演算を行うことで検出できます。この測定 はクロック・リカバリPLLが受けるような瞬間的なジッタ量を示 すため、重要になることがあります。周期ジッタとサイクル間ジッ タを計算するには、基準クロックの理想エッジ位置についての知 識は必要ありません。
図2.4aの測定TIE1〜TIE4にタイム・インターバル・エラーが示 されています。このTIEは、クロックのアクティブ・エッジがその 理想位置からどの程度ずれているかを測定します。この測定を行 うには、理想エッジが明らかであるか、または推定しなければな りません。このため、ある種のクロック・リカバリまたはポスト プロセッシングが行えない限り、オシロスコープで直接TIEを観察 するのは困難です。
TIEは、まず測定した各周期から公称(理想)クロック周期を引い た後の周期ジッタを積分して求めることもできます。TIEが重要な のは、少量の周期ジッタでさえ長期に渡ると、理想エッジからの 時間差が大きくなるという累積効果を示すためです。TIEが± 0.5UI(ユニット・インターバル)に到達すると、アイは閉じて、 レシーバ回路にビット・エラーが発生します。
図2.4cは、ある特定の波形に対してこの3つのジッタ測定を他の2つと比較した例を示しています。この例では、波形の公称周期は1μsですが、実際の周期は990nsのサイクルが8回続いた後に、1010nsのサイクルが8回続くパターンになります。
第3章:ジッタ測定とビジュアル化
ここでは、ジッタの定量化や解析に役立つツールやテクニックをいくつか説明します。
3.1 ジッタ統計
信号にはランダムな成分を持つジッタが含まれるので、ジッタを正確に評価するには統計的な手法が必要です。よく使用される手法には以下のものがあります。
平均値:クロック周期の相加平均値、つまり平均値は公称周期です。これは、周波数カウンタで測定する周波数の逆数です。TIEの平均値は理論的にはゼロですが、測定テクニックによっては小さな残差が出ることがあります。
標準偏差:ギリシア文字のシグマ(σ)で表される標準偏差は、測定値がその平均値からずれている平均量です。これは、平均と標準偏差で分布をすべて指定できるガウス・プロセスで表現されている場合に特に役立ちます。これについては、「4.3 複合ジッタ」で詳述します。
最大値、最小値、ピーク・トゥ・ピーク値:一般に、最大値と最 小値はインターバル測定中に実際に観測される値を言います。ピー ク・トゥ・ピーク値は、単に最大値から最小値を引いた値です。 これらの測定は適切に使用する必要があります。規則的に変化し ているデターミニスティック信号の場合、比較的短いインターバ ル測定の後でも、これらの値は真の値に等しくなることがありま す。しかし、ガウス分布を持つランダム信号の場合、理論的には 最大値、最小値に限界はないため、観測されたピーク・トゥ・ピー ク値は時間が経つにつれて増加します。このため、ピーク・トゥ・ ピーク値を使用する際には、母集団の大きさ、およびこの種の分 布に関する知識が必要です。
母集団:母集団は、統計上のデータ・セットに含まれる個々の測 定数(イベント数)です。ランダムなプロセスでは、母集団が大 きくなると、測定結果は再現可能であるという大きな信頼が直感 的に得られます。分布の特性が明らかな場合あるいは推定できる 場合、測定の不確実性を希望のポイント(設定値)まで減少させ るために必要な母集団を計算できます。
3.2 ジッタのヒストグラム
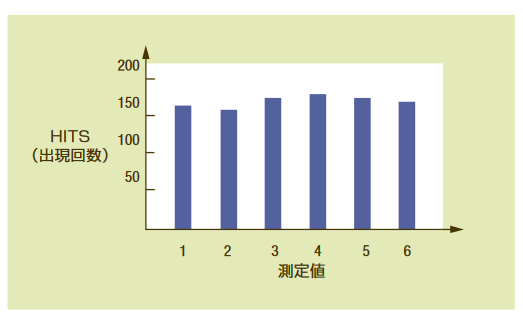
ヒストグラムは、データ・セットの測定値に対してその出現回数(測 定値の出現回数の分布)をプロットした図です。データ・セット の測定数が多い場合、ヒストグラムはこのデータ・セットのPDF(確 率密度関数)を正確に推定できます。たとえば、サイコロを 1,000回転がして、その結果を記録すると図3.2aのようになりま す。HITS軸はそれぞれの目の出現回数です。ヒストグラムは、観 測(測定)を行った順序に関連しないことに注意してください。
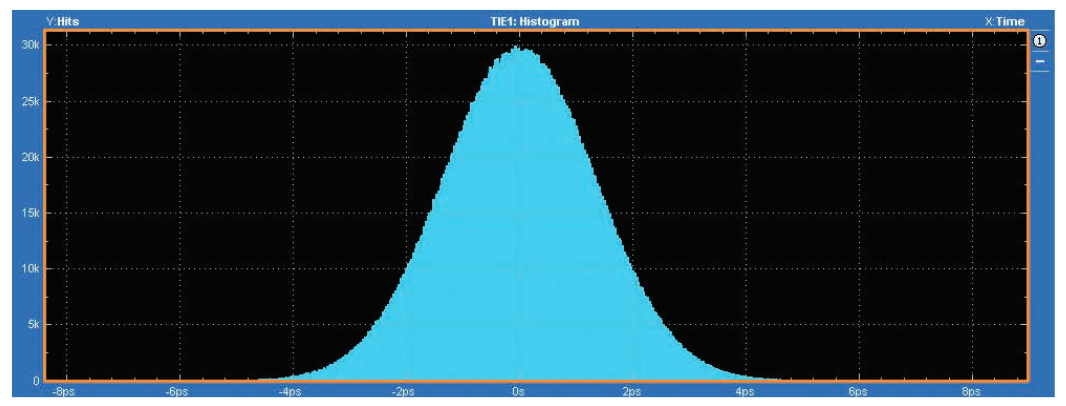
図3.2bは、TIE測定におけるジッタのヒストグラムの例を示して います。この場合、連続変数(分布の分割数)は500ビンにマッピン グされ、データ・セットの総測定値数(トータル・イベント数) は3,200,000です。これはTIE測定なので、平均値は0nsになり ます。このプロットでは、分布は標準偏差1.3psのガウス分布に ほぼなっています。
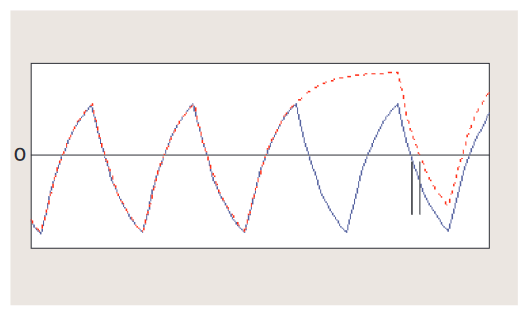
2番目の例を検討してみましょう。この例では、図3.2bの信号のTIEが、図3.2cに示されている正弦波で変調された場合を考えます。
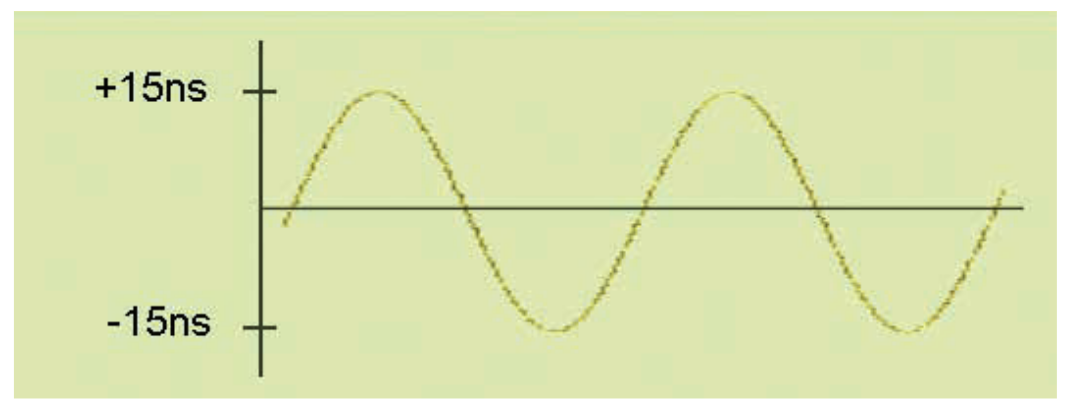
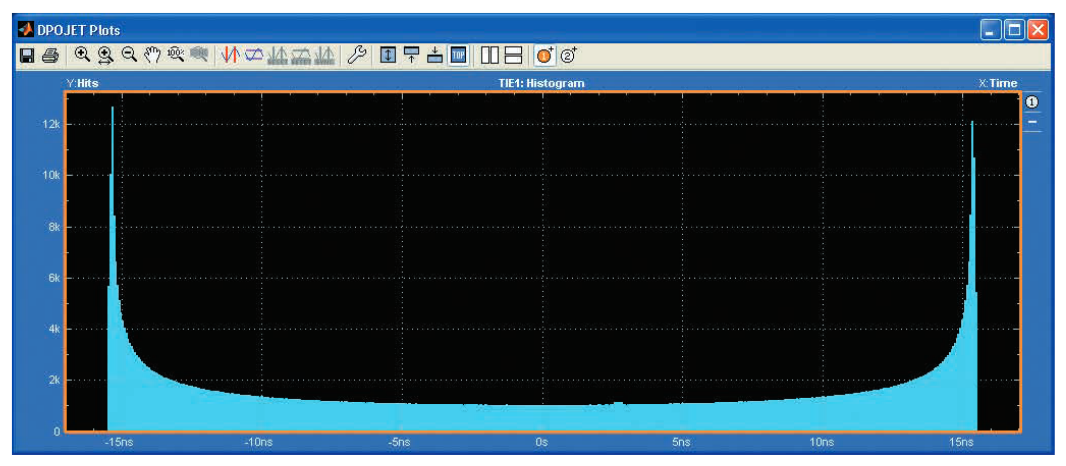
この正弦波が任意の時点でサンプリングされた場合は等尤度になり、サンプル値は−15ns〜+15nsの間のいたるところに存在します。したがって、この変調された信号のTIEヒストグラムは、図3.2dに示されているように、おおよそ等尤度で±15nsに広がります(ヒストグラムの左右にあるエッジの傾斜部分は、ジッタにまだガウス成分があることを示しています)。
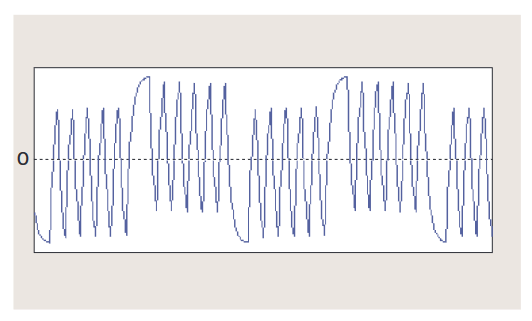
3.3 ジッタと時間(時間トレンド)
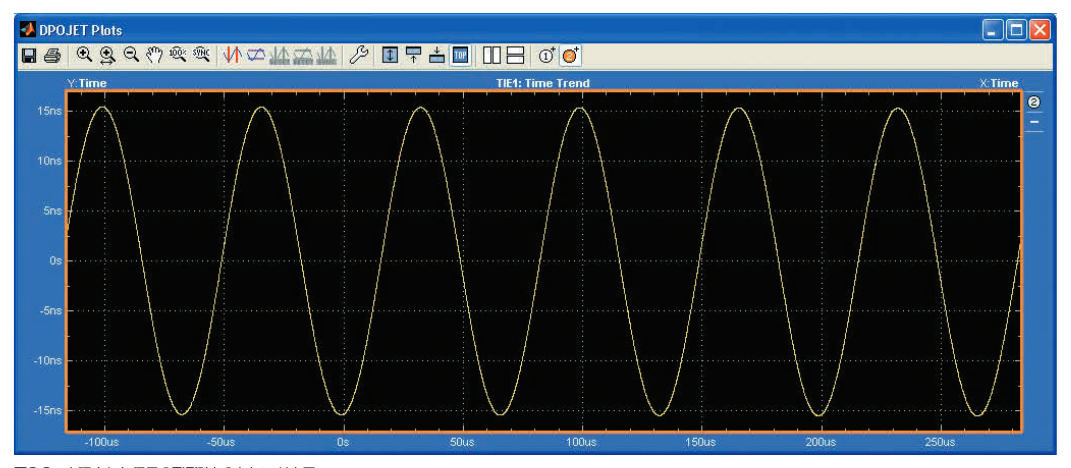
ジッタのヒストグラムには測定した順序が示されないため、変調 や他の周期性成分を示すような繰返しパターンは明らかになりま せん。時間に対するジッタ値のプロットから、これらの繰返しパ ターンが明らかになります。一例として、図3.2dの位相変調され た信号のTIEを時間に対してプロットすると、図3.3aになります。 これで、ジッタの変動パターンが明らかになり、いくつかあるジッ タ発生源の1つとの相関が明確になるかもしれません。
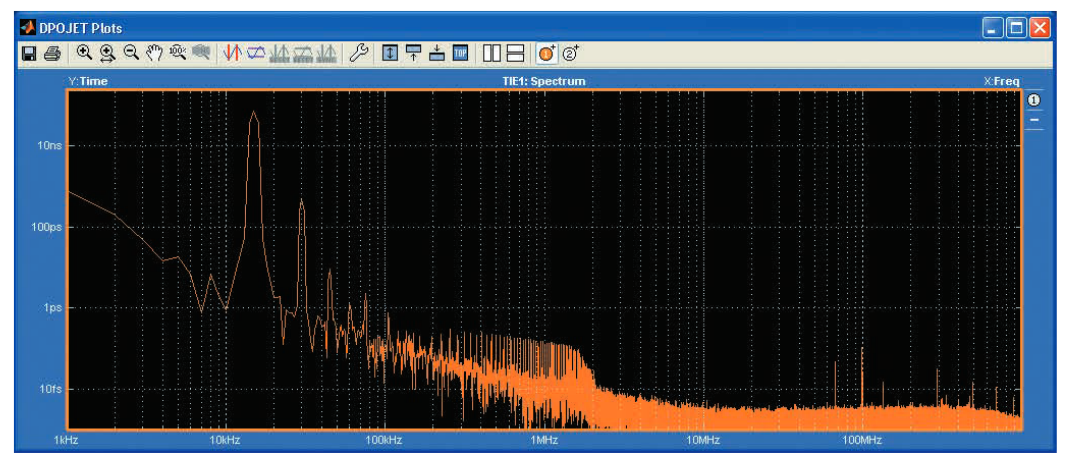
3.4 ジッタと周波数(ジッタ・スペクトラム)
ジッタ測定は時間に対してプロットできるので、これらの測定にフーリエ変換を適用すると、その結果を周波数領域で表示できます。これは、変調周波数を横軸に、変調の振幅を縦軸に表示したジッタ・スペクトラムになります。スペクトラム解析の利点の1つは、広帯域ノイズに隠れてしまうことがある周期性成分が、明確に識別できる場合が多いことです。
前述した正弦波変調で変調されたクロックの例をここでもう一度使用します。図3.4aは、図3.3aのTIE測定をスペクトラム解析した結果です。
これで、大きな突起状波形で示されているように、正弦波の変調 信号は15kHzの基本周波数を持つことが分かります。理論的には、 15kHzの正弦波のFFTには基本波成分しかありませんが、正弦波 変調されたクロックのTIEには歪も含まれているため、30kHz、 45kHz、60kHzの高調波成分が観測されます。ランダム・ノイズ はまだ出現しますが、この図では広範囲なフラット・ノイズ・フ ロアとして表示され、2MHz以上では平坦になっています。
前述したように、通常10Hzの制限を下回るフーリエ成分を持つタ イミング変動は、ジッタではなくワンダと見なします。さらに実 践面で重要なのは、その他の周波数制限(たとえば、システムの クロック・リカバリ・ループのループ帯域幅)によって、どのノ イズが安全に許容できるか決まる場合があることです。ジッタの スペクトラム表示で、システムのノイズが問題になるかどうか明 らかになります。
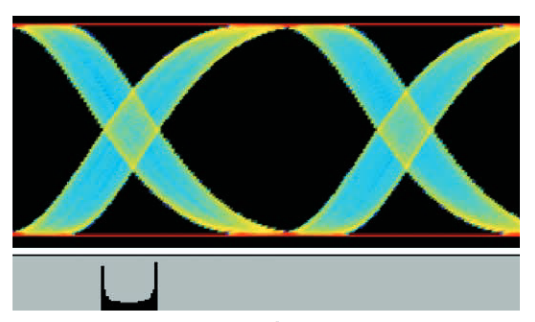
3.5 アイ・ダイアグラム
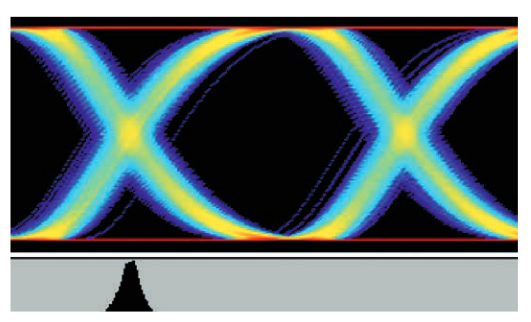
これまでに取り上げた方法はすべて、エッジ位置にのみ依拠しています。このエッジ位置は、波形がいつ1つ以上の振幅スレッショルドを横切るかを検出することにより、その波形から抽出されます。アイ・ダイアグラムは、波形の振幅動作とタイミング動作の両方を観測できる、より一般的なツールです。
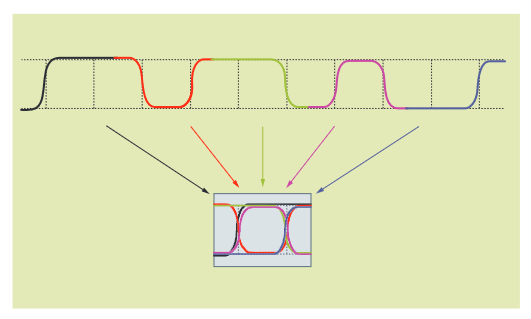
図3.5aに示されているように、波形の多くの短いセグメントを各 エッジの位置と電圧レベルがそれぞれ揃うように重ね合わせると、 アイ・ダイアグラムが作成されます。通常、水平方向のスパンを2 ユニット・インターバルにして表示されます。波形セグメントは、 図に示されているように、隣接していることもあり、また信号の サンプルをより広い間隔で取ることもあります。波形が繰返し信 号の場合、サンプリングを使用して、多くの波形上のランダム遅 延で得た個々のサンプルからアイ・ダイアグラムを作成できます。
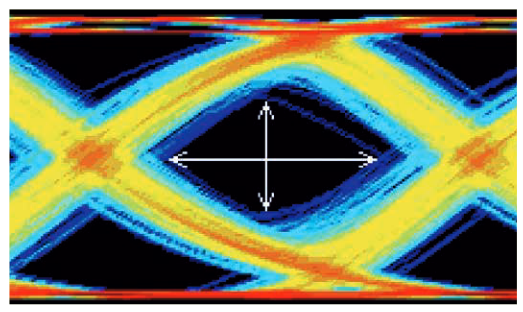
図3.5aでは、個々の波形セグメントがどのようにアイ・ダイアグ ラムを構成しているかを示すために、色を使用しています。実際 には、アイ・ダイアグラムは通常白黒、または色を使用して画面 上の任意の点における波形サンプル密度を示します。図3.5bは、 いくつかの種類のノイズを示す波形の色密度表示です。
図中の白い矢印はアイ開口部の縦方向と横方向の大きさを示しています。信号のノイズが大きくなると、アイの横方向、縦方向または両方向の開口部は小さくなります。図の中心に開いた部分がなくなると、アイは閉じているといいます。
アイ・ダイアグラムを作成する最も簡単な方法は、オシロスコー プを長時間のパーシタンス表示モードで使用することです。この アプローチでは、どのようにトリガをかけるかに注意する必要が あります。単に波形のエッジでトリガをかけると、そのエッジを 基準として波形を示すアイ・ダイアグラムになります。これは、 基本的なビット・クロックを基準にしたアイ・ダイアグラムとは 大きく異なることがあります。ビット・クロックを基準にしたダ イアグラムを作成するには、ソフトウェアまたはハードウェアの いずれかで何らかの形のクロック・リカバリが必要です。使用す るオシロスコープにこの機能がなければ、外部のクロック・リカ バリ回路からトリガを与えます。
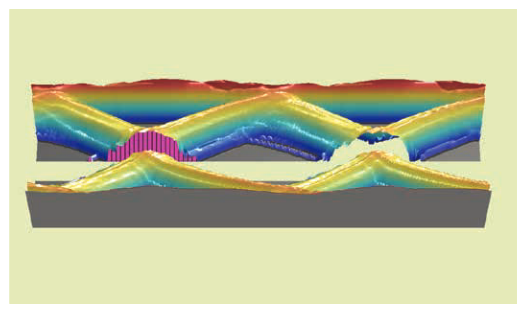
アイ・ダイアグラムとTIEヒストグラムの関係は、図3.5bの密度アイ・ダイアグラムを3次元グラフに変え、図3.5cに示されているように、決定スレッショルドに沿ってスライスすることで見ることができます。ピンク色の部分は、アイ・ダイアグラムに2つあるゼロ・クロス点の最初のヒストグラムと等しくなります。
第4章: ジッタの分離
「モデルはみな間違っている。中には役立つものもある」W. Edwards Deming
ジッタの分離、またはジッタの分解は、パラメータ化したモデルを使用して、システム動作を記述および予測する解析方法です。本章では、なぜこの方法を使用するのかを説明し、今日最もよく使用されているジッタ・モデルについて詳述します。
4.1 ジッタを分解する目的
実際のシステムがどのように動作するかを理解するために、シス テムの数学モデルを使用すると役立つことがよくあります。こう したモデルの動作は、各コンポーネントのパラメータを調整する ことによって調節できます。モデルのパラメータが実際のシステ ムの観測に基づいて選択された場合、そのモデルを使用して他の 状況でもシステムの動作を予測できます。したがって、ジッタ分 解(ジッタの分離とも言います)の目的の1つは、直接測定するの が困難か、あるいは時間がかかる場合、システム性能を推定する ことです。
システムをこのようにモデリングするもう1つの目的は、解析に関係しています。各モデル・コンポーネントが複数の基本的な物理的効果と関連している場合、モデルを理解することにより、過度のジッタの原因を正確に見極められます。
複雑なシステムのモデルはすべて、推測を立て簡略化されるため、モデルと実際のシステム動作との適合度は正確ではありません。実際、モデルの動作を実際に行う測定と合わせる場合、パラメータの選択には常にいくらかの許容範囲があります。このため、ジッタの分離には技術的および科学的な要素がいくらかあり、測定の「99.99%」の再現性は考えられません。
4.2 ジッタ・モデル
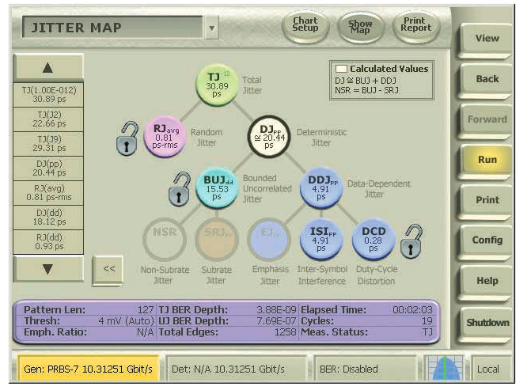
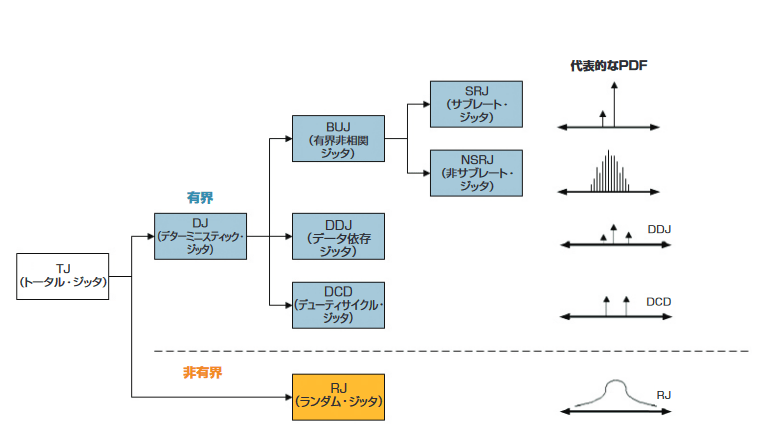
最もよく使用されているジッタ・モデルは、図4.2に示されている階層に基づいています。この階層では、最初にトータル・ジッタ(TJ)をランダム・ジッタ(RJ)とデターミニスティック・ジッタ(DJ)の2種類に分けます。この2種類のジッタを正確に識別するかどうかは、他のモデリング決定より、モデルの正確さに著しい影響を与えます。
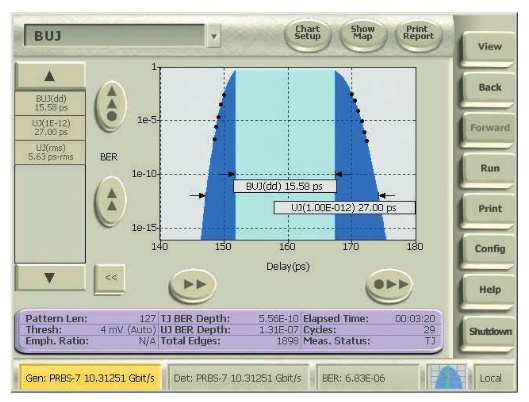
デターミニスティック・ジッタをさらに、周期性ジッタ(PJまた は正弦波ジッタ、SJということもあります)、デューティ・サイク ル依存ジッタ(DCD)、データ依存ジッタ(DDJまたはシンボル 間干渉、ISIということもあります)、有界非相関ジッタ(BUJ) に分けます。BERTScopeのBER等高線機能で表示されるBUJの 値の様子を図4.2aに示します。
これらのジッタそれぞれの特性と根本原因については後述します。
4.2.1 ランダム・ジッタ
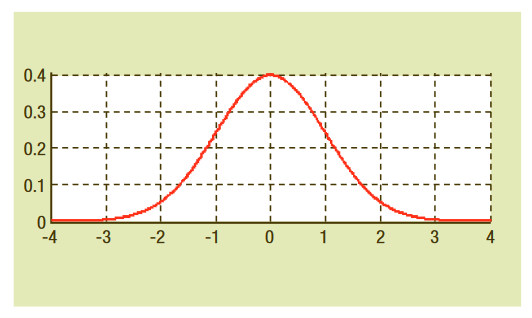
ランダム・ジッタは、識別可能なパターンがないため、予測でき ないタイミング・ノイズです。ランダム・ノイズの代表例としては、 無線受信機を搬送周波数に合わせたときに聞こえる音があります。 ランダム・プロセスが理論的に確率分布する場合、ジッタ・モデ ルの目的上、ランダム・ジッタはガウス分布を持つと推定されます。 この理由の1つは、多くの電気回路におけるランダム・ノイズの主 な発生源は、熱ノイズ(ジョンソン・ノイズ、ショット・ノイズ と言うこともあります)で、ガウス分布することが知られている ためです。さらに根本的な理由は、多くの相関しないノイズ発生 源の複合した影響は、個々のノイズ発生源の分布に関係なく、中 心極限定理に従ってガウス分布に近付くことです。
正規分布とも言われるガウス分布には、おなじみのベル曲線で表 されるPDFがあります。図4.2.1aは、平均値ゼロ、標準偏差1.0 のガウス分布の例です。この分布については、参考文献4の1つに 詳細に取り上げられていますが、その最も重要な特性は、ガウス 変数のピーク値は無限であることです。すなわち、このランダム 変数のほとんどのサンプルは平均値周辺に集まりますが、ある特 定のサンプルは理論的にその平均値と大きく異なることがありま す。したがって、基礎になる分布には制限されたピーク・トゥ・ピー ク値はありません。こうした分布から取ったサンプルが多くなれ ばなるほど、測定したピーク・トゥ・ピーク値は大きくなります。
何回も繰返しサンプリングし、その結果のピーク・トゥ・ピーク 値を記録することにより、こうした分布を評価しようとする方法 があります。このアプローチには注意が必要です。ランダム変数 のN回測定したピーク・トゥ・ピーク値は、たとえ標準偏差の低い 変数であっても、それ自体がランダム変数です。たとえば、品質 検査の合否基準としてこのようなランダム変数を使用すると、測 定が不確実なため、合格スレッショルドを上げる必要があり、結 果として、許容できる製品まで不合格になってしまいます。推定 した分布(この場合、ガウス分布)にN回の測定値を合わせるアプ ローチの方が優れています。これにより、分布の数理表現を使用 してより長期の動作を特定の信頼レベルまで予測できます。
図4.2.1bは、ガウス・ジッタのみを持つ信号のアイ・ダイアグラムと関連するTIEヒストグラムを示しています。
4.2.2 デターミニスティック・ジッタ
デターミニスティック・ジッタは再現のある予測可能なタイミング・ジッタです。このため、このジッタのピーク・トゥ・ピーク値は制限され、通常この制限はかなり少ない回数の測定に基づき、高い信頼度で観測・予測できます。この種のジッタは、ジッタの特性と根本的な原因によって以下のように分類されます。
4.2.3 周期ジッタ
周期的に繰り返されるジッタを周期ジッタと言います。図2.4cに例を示します。TIEの時間トレンドは繰り返し三角波を表しています。周期波形は、フーリエ級数で正弦波の高調波に分解できるため、この種のジッタを正弦波ジッタと言うことがあります。図4.2.3aは、ピーク振幅1.0の正弦波の確率分布を示しています。
一般に、周期ジッタはデータ・ストリームで周期的に繰り返されるパターンと相関しません。繰り返しデータ・パターンと相関するジッタについては、次の節で取り上げます。周期ジッタは、スイッチング電源のノイズや強力なローカルRFキャリアのようなシステムに結合する外部デターミニスティック・ノイズ源によって生じます。また、不安定なクロック・リカバリPLLも原因になります。
図4.2.3bは、0.2UIの周期ジッタがある信号のアイ・ダイアグラムとそれに関連するTIEヒストグラムを示しています。
4.2.4 データ依存ジッタ
データ・ストリームのビット・シーケンスと相関するジッタをデー タ依存ジッタまたはDDJと言います。DDJは、ケーブルやデバイ スの周波数応答によって発生することがよくあります。図4.2.4a の波形を検討してみましょう。データ・シーケンスが強力にロー・ パス・フィルタリングされています。このフィルタリングのため、 同じ極性が数ビット連続しない限り、波形は完全なハイまたは ロー・ステートに達しません。
図4.2.4bは、データ・シーケンスの異なる波形を重ね書き表示したものです。立下りトランジションは、1,0,1,0,1,1,1シーケンスが後に続く時より、1,0,1,0,1,0,1シーケンスが後に続く時の方が、先にスレッショルド・レベルを横切るのが観測できます。
このタイミング・シフトは予測可能で、トランジション前の特定のデータに関係することから、DDJの一例と言えます。これは、シンボル間干渉、ISIとも言います。
図4.2.4cは、0.2UIのDDJを持つ信号のアイ・ダイアグラムと関連するTIEヒストグラムを示しています。ISIジッタのヒストグラムは常にインパルスのみで構成されます。
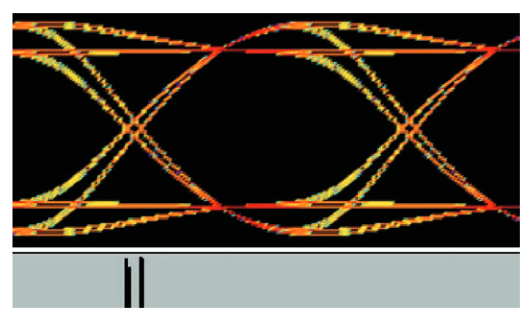
4.2.5 デューティサイクル依存ジッタ
関連するエッジが立上りか立下りかによって予測できるジッタをデューティサイクル・ジッタ(DCD)と言います。DCDの原因としてよくあるものは、以下の2つです。
- 1. 立上りエッジのスルー・レートが立下りエッジと異なる。
- 2. 波形の決定スレッショルドが、あるべき位置より高いまたは低い。
図4.2.5aは、最初のケースを示すアイ・ダイアグラムです。決定 スレッショルドは50%振幅ポイントにありますが、波形の立上り 時間が遅いため、立上りエッジは立下りエッジより後でスレッショ ルドを横切ります。この結果、エッジ交差(灰色)のヒストグラ ムは2つの異なるグループを示します(前のアイ・ダイアグラムと 異なり、この例の波形にはデューティサイクル依存ジッタの他に ガウス・ノイズがあります)。
図4.2.5bは、2番目のケースを示すアイ・ダイアグラムです。波形の立上り時間と立下り時間はバランスがとれていますが、決定スレッショルドは50%振幅ポイントに設定されていません。エッジ交差のヒストグラムは、図4.2.5aに示されているヒストグラムに非常によく似ています。
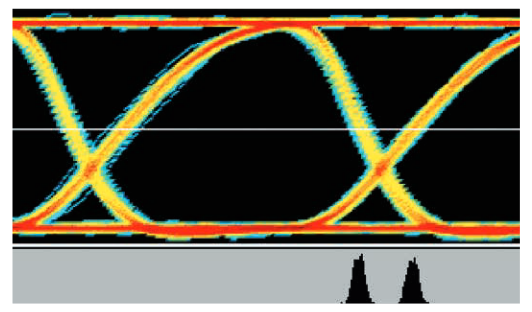
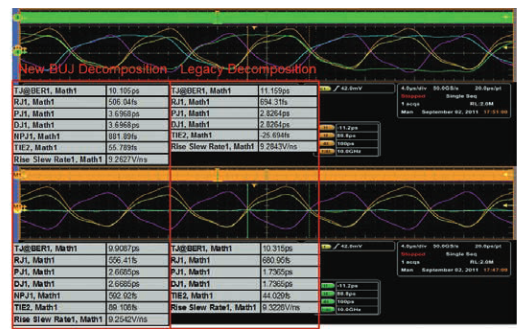
4.2.6 BUJ(Bounded, Uncorrelated Jitter、有界非相関ジッタ)
4x10GbEなどの高速インターコネクトで見られる隣接した チャンネル間のクロストークは、シリアル・リンクの性能に大き く影響します。また、クロストークは従来のジッタ分離手法の確 度を損ない、ランダム・ジッタの過度の計算により高速リンク・ デバイスの設計マージンが小さくなります。ジッタ分離によって 得られるBUJ(有界非相関ジッタ)により、結果として得られる BERのアイ合成がより正確に評価できます。図4.2.6に示すよう に、隣接チャンネルで構成される高周波シリアル・リンクにおけ るジッタは改善されます。
4.2.7 SRJ(Subrate Jitter、サブレート・ジッタ)
デターミニスティック・ジッタは、しばしば近傍のロジック処理 が原因となってシステムに発生します。このような相互作用で生 ずるジッタは同期または非同期であり、BUJ(データ・パターン と相関性がないので「非相関」となります)のカテゴリに分類さ れます。クロックに同期するジッタは特殊であり、この種のジッ タの代表的なケースです。マルチプレクス/デマルチプレクス、 チャンネル・コーディング、ブロック・フォーマット、低速のパ ラレル処理などの信号処理はすべて、整数のクロック境界におい てエッジをシフトさせる可能性があります。
図4.2.7に示す、トランスミッタの4 : 1マルチプレクサは、並列 負荷のすべてのレジスタの4で割り切れるエッジのタイミングを早 めたり、または遅らせたりします。1/4のクロック・レートでト リガされたアイ・ダイアグラムでは、2つのアイは正常のアイ幅を 持ち、ジッタのあるエッジ周辺で1つは短いアイ幅、1つは長いアイ幅になります。これは、パターンのすべてのビットで観測でき るので(パターン長が4の倍数でない限り)、ISIとは解釈されま せん。
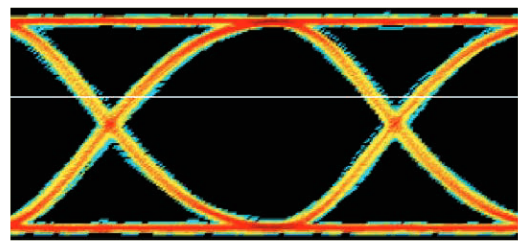
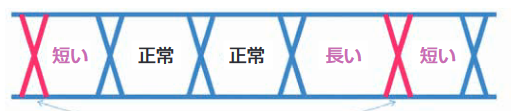
すべてのアイの平均遷移回数における、高調波に関係ない差異で、上記の分割比になるものは分割比と相関性のあるデターミニスティック・ジッタであり、これはSRJ(Subrate Jitter、サブレート・ジッタ)と報告されます。SRJの数よりも大きなBUJは、さらにNSR(Non-Subrate Jitter、非サブレート・ジッタ)と呼ばれます。
SRJとパターン依存性のISIは、間違えやすいので注意が必要です。測定されるデータ・パターンがサブレート分周の倍数ちょうどである場合はISIの成分と認識されるため、サブレートで見られるジッタはSRJの数には含まれません。
4.3 複合ジッタ
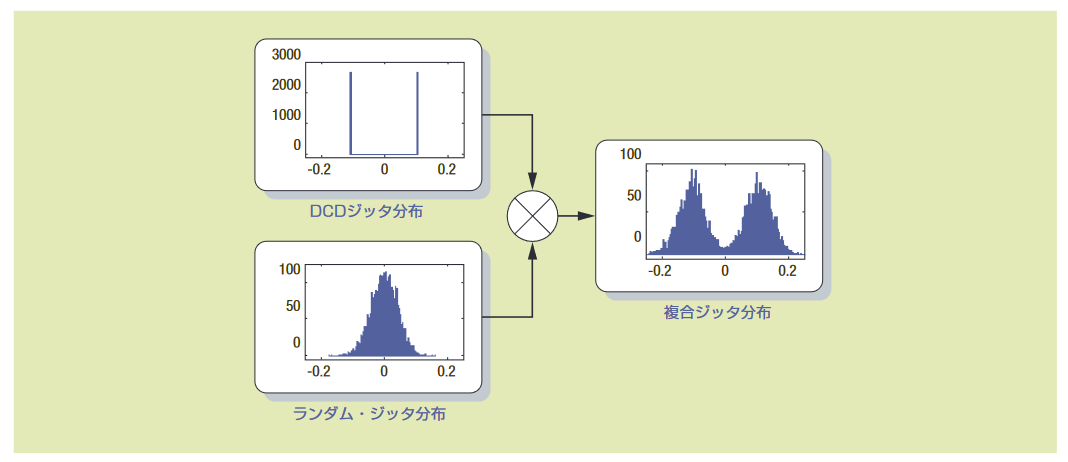
これまでに、各種ジッタのアイ・ダイアグラムとTIEヒストグラム について述べてきました。しかし、同時に複数の種類のジッタが 発生した場合、ヒストグラムはどうなるでしょうか?複数のラン ダム・プロセスが互いに関連していない場合、それぞれの結果の 合計による分布は、個々の分布のコンボリューション(畳込み積分) に等しくなるというのが、統計理論から得られる有効で応用可能 な結果です。
この考え方は、文字で説明するより、ビジュアルで表現した例の 方が理解しやすくなります。図4.3aは、デューティサイクル依 存ジッタ(2つのインパルスで構成されるヒストグラムを持つ)が ランダム・ジッタ(ガウス分布を持つ)と一緒になったとき何が 起こるかを表しています。図3.2dにもその一例が示されています。 この図では、正弦波の分布(周期ジッタの分布と同じ)がランダム・ ジッタと競合しています。
理論的には、図4.3aの最終的なヒストグラムを観測して、2種類のジッタが何を引き起こすかを推測できます。しかし、実際の例ではすべての種類のジッタがさまざまな量で含まれるので、直感的に認識しにくい複雑なヒストグラムになります。詳細なジッタ解析の目的の1つは、最終的な結果の原因になる個々のジッタ成分をすべて明らかにすることです。
ジッタの分離は、正確に特定されたジッタ成分を図4.2に示すジッタ・モデルに当てはめ、モデルを使用して新しい環境でシステムがどのように動作するかを予測するときに、真の力を発揮します。これはビット誤り率の推定の基礎で、これについては第5章で詳述します。
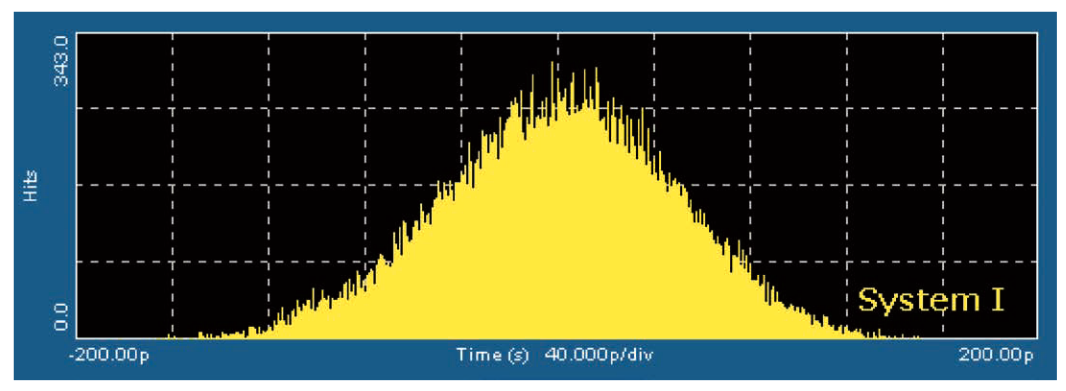
なぜ正確な解析ツールが重要なのかを理解するために、異なるジッ タ特性を持つ2つのシステムを比較します。最初のシステムをシス テムIとします。このシステムには、標準偏差が0.053UIのランダ ム・ジッタだけがあります。1062.5Mbpsのデータ・レートを持 つこのシステムのTIEヒストグラムを図4.3bに示します。
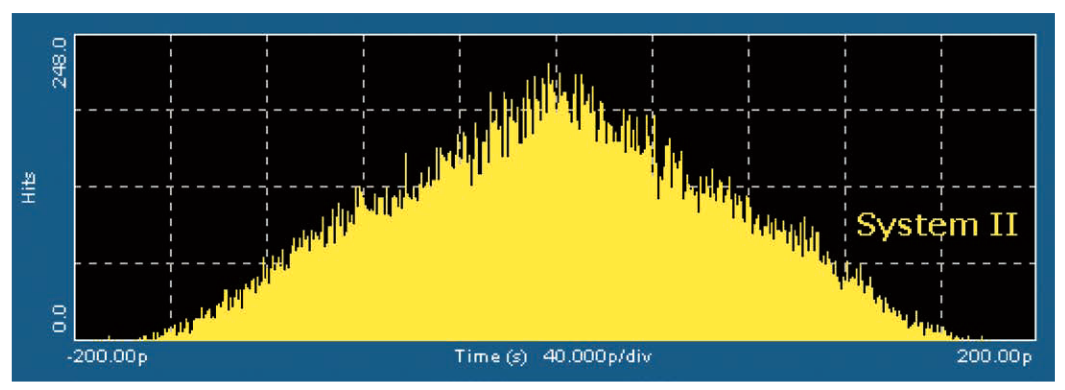
2番目のシステムをシステムIIとします。このシステムには、標準偏差が最初のシステムの約2分の1に当たる0.028UIのランダム・ジッタがあります。ただし、このシステムには、相関のない2つの周期ジッタの成分もあり、それぞれのピーク・トゥ・ピーク振幅は0.14UIです。図4.3cは、システムIIのTIEヒストグラムを示しています。
約42,000エッジという同じイベント数のこの2つのヒストグラム は、それほど違いがあるように見えません。実際、この2つのサン プル・セットについては、タイム・インターバル・エラーのピーク・ トゥ・ピーク値は、ちょうど同じ430ps(0.457UI)です。視 覚的な比較が利用可能な唯一の方法である場合、この2つの場合の 識別は困難になります。長時間に渡る測定インターバルの間、シ ステムがどのように動作するかを正確に予測できません。
この2つの場合はこれほどよく似ているのだから、区別することが重要なのかと、疑問に思うかもしれません。ビット誤り率とバスタブ曲線について説明した後、この例を再度取り上げます。
第5章:ジッタとビット誤り率
「正しい質問に対するおおよその答えは、おおよその質問に対する正確な答えより大いに価値がある」
John Tukey
5.1 ジッタ・バジェット
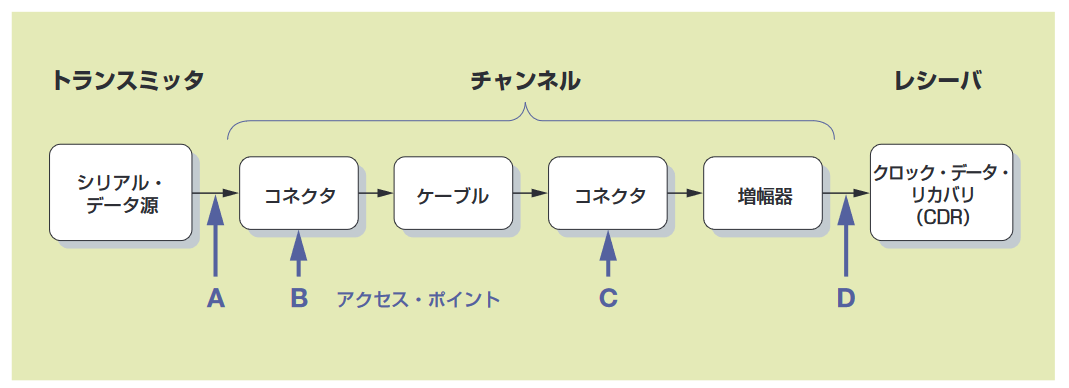
実際の通信システムは、図5.1のモデルのように、トランスミッタ、 チャンネル、レシーバから構成されています。チャンネルには、 ケーブル、インターコネクト、クロック再生を行わないアクティブ・ デバイスが含まれることがあります。チャンネルは、フィルタリン グ、非直線性、DCオフセット、インピーダンスの不一致、さらな るランダム・ジッタを導くことがあります。さまざまな回路テスト・ ポイントやシステム・コネクタは、信号の品質を評価するアクセス・ ポイントになります。このシステムはトランスミッタからレシー バに進みにつれ、各アクセス・ポイントで(おそらくアイ・ダイ アグラムを使用して)信号品質を順番に評価すると、信号のジッ タは一般に劣化します。
単純に、信号がレシーバのクロック・データ・リカバリ回路の入 力(アクセス・ポイントD)に到達した時に、アイが少しでもまだ 開いていれば成功であると推測できます。しかし、レシーバ回路 は完全ではありません。受け取った信号のアイは、レシーバのデー タ確定回路のタイミング・マージンを確保できるようにするため には水平方向に十分に開き、しかも決定スレッショルドに影響を 与えるノイズに対応できるようするには垂直方向に十分に開いて いなければなりません。
したがって、完全なシステム設計仕様は、明確に定義された各アクセス・ポイントが既知のジッタ・リミットを持ち、再同期させるレシーバに信号が入るときに十分なマージンが残るように、ジッタ・バジェットを割り当てます。
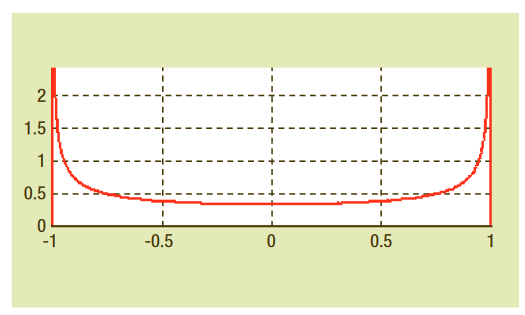
5.2 バスタブ曲線
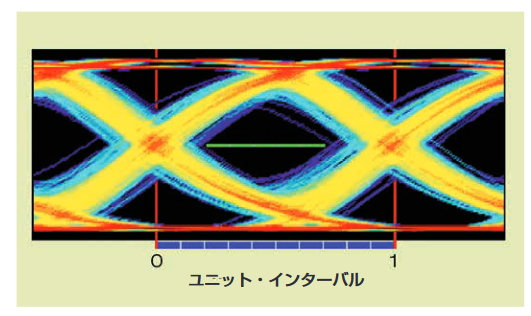
アイ・ダイアグラムとアイ開口の考え方については「3.5 アイ・ ダイアグラム」で説明しました。理論的には制限されていないピー ク・トゥ・ピーク値を持つガウス確率分布については、「4.2.1 ラン ダム・ジッタ」で取り上げました。この2つを一緒に検討すると、 興味深い考えが生まれます。ガウス・ジッタを持つ信号については、 十分に長い時間サンプルを累積するとアイ・ダイアグラムは完全 に閉じます。これにより、比較の基礎としてアイ開口の考え方は 役に立たなくなります。しかし、信頼評価レベルをアイ開口に適 用することで、アイ・ダイアグラムを活用できます。
図5.2aについて検討しましょう。長さが0.5UIの緑色のルーラーは、アイの中心に水平方向に配置されています。波形が立上りであれ、立下りであれ、このルーラーと交差するとエラーとみなすと仮定します。この図では、波形はこのルーラーとまだ交差していないように見えますが、波形サンプルを累積し続け、この信号にガウス・ジッタがある場合、波形は必ずルーラーと交差します。
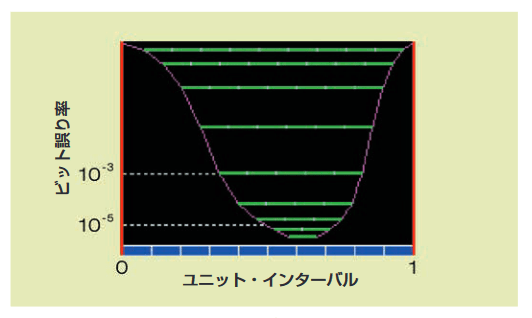
その代わりに、ルーラーと交差する波形が1,000個にわずか1個 の場合、テストは成功と見なすと仮定します。テストがどれほど 長くかかろうと、もはや問題ではありません。50,000波形が累 積でき、50以下の波形がルーラーと交差した場合、テストは合格 になります。103に1個の波形が交差し、アイは50%(0.5UI) 開いていると言えます。それぞれの交差がビット・エラーを表し ていると推定されるため、これはBER(ビット誤り率)10−3にな ります。
同じ信号を短いルーラー、例えば0.25UIの長さでテストした場合、ルーラーと交差する回数は確実に減少します。おそらく、平均して100,000に1個の波形がこの短いルーラーと交差します。105に1個の波形が交差し、アイは25%(0.25UI)開いていると言えます。
この方法でルーラーを使用して、ビット誤り率に対するアイ開口を正確に評価できます(各ルーラーは、最良の適合性を得るため、左右にスライドできることに注意してください)。すべてのルーラーを1つのチャート上に対応するビット誤り率に対してプロットし、ルーラーの端を線で結ぶと、図5.2bのようなグラフになります。
ピンク色の線はバスタブのように見えるので、この分布のグラフをバスタブ曲線と言います。このグラフを使用すると、与えられた信頼レベルに対し、アイの水平部に信号のトランジションが発生しない領域がわかります(アイ開口の大きさがわかります)。
最後に、チャートの底辺近くのアイ開口を直接測定するために十分なデータを累積するには、長時間かかる可能性があることに注意してください。このため、第4章で取り上げた数学モデルを使用して、はるかに小さなサンプル・セットに基づいて性能を予測します。
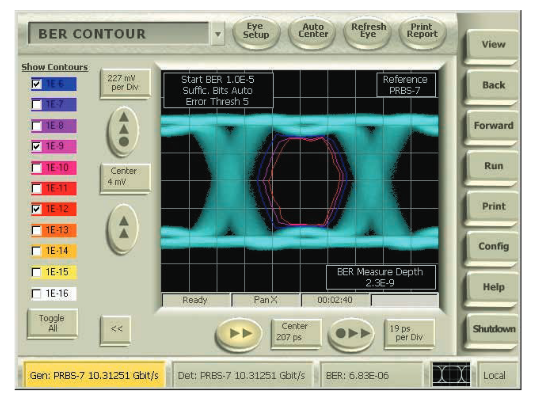
特定のBERレベルでのジッタ性能の特定に役立つもう一つの概念が、BER等高線のプロットです。BER等高線(図5.2c)はバスタブ曲線の拡張機能であり、アイ開口を放射状に測定し、特定のBERレベルにおけるアイ開口をわかりやすく表現しています。
5.3 BER の例
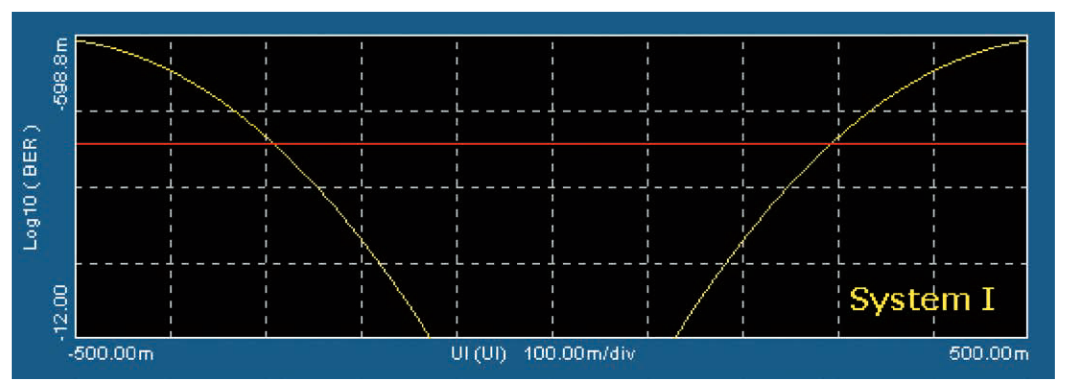
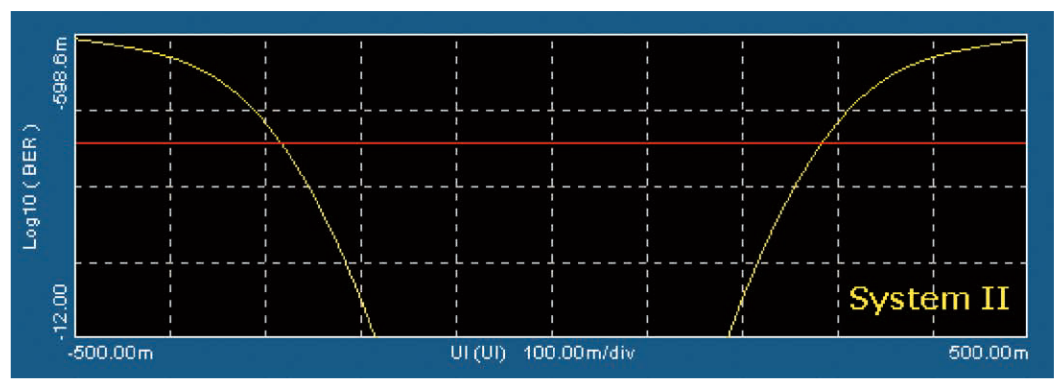
「4.3 複合ジッタ」で、異なるジッタ特性を持つ2つのシステムは、約42,000エッジのサンプル・サイズでは、ほぼ同じTIEヒストグラムと同一のピーク・トゥ・ピーク・ジッタ特性を持つ例を取り上げました(図4.3b、4.3c参照)。ここで、その例に戻り、関連するバスタブ曲線を示します。図5.3aはシステムIのバスタブ曲線、図5.3bはシステムIIのバスタブ曲線を示しています。
これらのグラフは両方とも観測した42,000エッジのデータ・セッ トを表し、赤いカーソルは各グラフ上の42,000分の1、すなわち 10−4.63のBERに対応する位置に配置しています。これらのレベル では、システムは両方とも約58%のアイ開口を示し、実際にはシ ステムIのアイ開口はシステムIIより大きくなっています。しかし、 BER 1e-12(シリアル通信リンクでは頻繁に使用される規定ポ イント)では、システムIのアイはわずか26%開いているだけです。 システムIIのアイは37%開いています。これはシステムIの約1.5 倍です。これは重要な差異で、システムが規定されたBERに対し て仕様を満たしているかどうかを簡単に判断できます。
第6章:まとめ
タイミング・ジッタは常に電気システムを劣化させますが、より高速のデータ・レートと、より小さい論理幅を目指すために、その評価の重視性が高まっています。ジッタの原因を特定して再設計で減少させるために評価が必要です。規格遵守および設計仕様のためのジッタの定義、特定、測定にも役立ちます。
ジッタには、ランダムおよび規則的な成分があります。そのラン ダムな性質のため、ジッタの許容可能な制限を指定する際には注 意が必要です。これは特に低いエラー・レートにおけるジッタの 性能を、比較的少ないデータ量に基づいて予測する場合に該当し ます。ジッタのランダム成分を処理するために、ジッタの解析と 予測に適した方法は数学モデルを使用することです。そのパラメー タは観測された測定結果に基づいて調整されます。このモデルは、 他の状況での性能を予測するために使用できます。また、このモ デルからジッタの原因を明らかにできるため、どのような成分の ジッタを減少させるかを理解するために役立ちます。
以前より、オシロスコープは、ヒストグラム、アイ・ダイアグラ ムなどの技法を使用してジッタを観測するためのツールでした。 サイクル・トゥ・サイクル測定、時間トレンドおよびスペクトラ ムのプロット、データ・ロギング、ワースト・ケースの取り込み などの機能を追加するバック・エンド・プロセッシングによって 強化されたオシロスコープは、タイミング・ジッタを評価するた めの最適なツールです。また、高度なクロック・リカバリ、ジッ タ分離アルゴリズム、ビット誤り率の予測をさらに強化されたオ シロスコープは、タイミング・ジッタを評価し、減少させるため の唯一のソリューションになります。
ジッタ測定に最適なオシロスコープ
タイミング・ジッタを測定、評価、減少させるための唯一のソリューション、最新のオシロスコープをご紹介します。
5シリーズB MSOミックスド・シグナル・オシロスコープ
忠実度に優れた波形、多彩な測定表示、独自のスペクトラム解析、柔軟なプローブ技術により、設計の全体像を把握することができます。世界中のエンジニアに支持されている、直感的なユーザ・インタフェースをご体験ください。
6シリーズ B MSOミックスド・シグナル・オシロスコープ
1GHz~10GHzの帯域幅での高速設計のトラブルシューティング/検証。低ノイズ、最大50GS/sのサンプル・レートで正確な測定を実現します。6チャンネル/8チャンネルの機種で設計のより詳細な解析が可能です。
DPO70000SX ATIパフォーマンス・オシロスコープ
DPO70000SXシリーズATIパフォーマンス・オシロスコープは、高速な信号の挙動を優れた確度で取り込めるため、次世代設計の検証、動作確認、特性評価に最適です。最高70GHzの信号を低ノイズと優れた忠実度で取り込めるため、高確度な測定が可能になり、信号の特性を正確に把握することができます。
付録 A:略語解説
BER ビット誤り率
BUJ Bounded, Uncorrelated Jitter、有界非相関ジッタ(境界のある、相関性のないジッタ)
CDF 累積分布関数
DCD デューティサイクル依存ジッタ
DDJ データ依存ジッタ
DJ デターミニスティック・ジッタ
FFT 高速フーリエ変換
ISI シンボル間干渉
NSRJ Non-Subrate Jitter、非サブレート・ジッタ
PDF 確率密度関数
PJ 周期ジッタ
PLL フェーズ・ロック・ループ
PSD パワー・スペクトル密度
RJ ランダム・ジッタ
SJ 正弦波ジッタ
SRJ Subrate Jitter、サブレート・ジッタ
TIE タイム・インターバル・エラー
TJ トータル・ジッタ
UI ユニット・インターバル