Question :
How can I measure and calculate nV/Root Hz (nanovolt per root Hertz) on a spectrum analyzer?
Answer :
Spectral Noise Measurements
The relation of dBm/Hz in 50 Ohms and nV/Root Hz in 50 Ohms.
Spectrum Analyzers are calibrated with very accurate CW signals (using a signal generator, a power splitter, and a power meter). The calibration is done at many frequencies to correct for frequency response of the analyzer. The signals are pure sine waves, and the calibration is in RMS.
Noise measurements are based on the CW RMS power calibration, the noise bandwidth of the measuring filter (RBW), and a calculation to normalize from the noise bandwidth to 1 Hz. To normalize from X Hz to 1 Hz:
- dB = 10 log (X Hz/1 Hz).
FFTs do not use any of the log circuitry or envelope detector circuitry of classical spectrum analyzers (instead, log and envelope is done in math). Therefore, the 2.5 dB log and detector error correction factor required in classical spectrum analyzers is not needed in FFT spectrum analysis.
- When spectrum analyzers give a result in dBm/Hz, the meaning is dBm/1Hz, into 50 Ohms. This is in RMS.
- Op Amp or JFET noise specs are given in nV/Root Hz, it is nV/Root (1Hz). This is in RMS.
Both A and B above are in 1 Hz, even though the readouts, and specs in printed device data sheets leave out the 1 (the 1 is silent).
But Root (1 Hz) = 1 Hz. So, as long as we stay in 1 Hz, we can easily convert from dBm/Hz in 50 Ohms to nV/Root Hz in 50 Ohms.
The Spectrum Analyzer "Channel Power" measurement feature can be used to integrate the power over a user specified bandwidth, even though the measuring bandwidth is different. This is just a re-application of formula # 1. above.
dB = 10 log (X bandwidth/Y bandwidth), where X is the channel bandwidth and Y is the measuring bandwidth.
Below is a screen shot of a measurement of a relatively flat noise floor, using an RSA3408A. An explanation of the various readouts are given below:
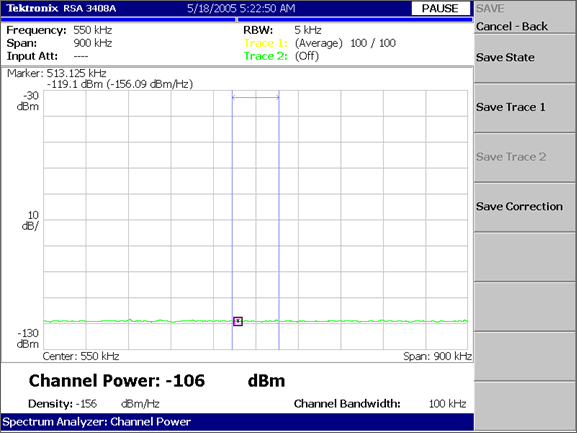
The RBW (measuring filter noise bandwidth) is 5 kHz.
The Marker Value in that 5 kHz bandwidth is -119.1 dBm.
The Marker Value in 1 Hz is -156.09 dBm/Hz.
The (integrated) Channel Power in 100 kHz bandwidth is -106 dBm.
The average noise density in the 100 kHz bandwidth is -156 dBm/Hz. (/1 Hz)
The (user defined) 100 kHz Channel is indicated by the vertical Blue lines near the center of the graph.
To calculate from one readout to the other:
dB from 5 kHz to 1 Hz = 10 log (5x103/1) = 36.99 dB. So, there is 36.99 dB less (-) noise in 1 Hz than 5 kHz. -119.1 dBm/5kHz -36.99 dB = 156.09 dBm/Hz (the dBm/Hz Marker).
dB from 100kHz to 1 Hz = 10 log (1x105/1) = 50 dB. There is 50 dB more (+) noise in a 100 kHz channel than in 1 Hz. -156 dBm/Hz + 50 dB = -106 dBm in 100 kHz (the Channel Power reading).
The (average) Density in the 100 kHz channel is -156 dBm/Hz. And that agrees with the Marker dBm/Hz and the above calculations.
The noise floor is -156 dBm/Hz; To calculate nV/Root Hz:
1000 mW = 1 Watt; +30 dBm = 0 dBW; -30 dBW = 0 dBm
So, -156 dBm - 30 dB = -186 dBW
W = 10dBW/10
W = 10-186/10
W = 10-18.6
W = 2.512 x 10-19
W = E2/R
W = E2/50
50 x W = E2
Root (50 x W) = E
Root (50 x 2.512 x 10-19) = 3.544 nV
-156 dBm/Hz = 3.544 nV/Root Hz
FAQ ID 57266
View all FAQs »
