Abstract
This paper provides an introduction to the BER Contour measurement - what it is, how it is constructed, and why it is a valuable way of viewing parametric performance at gigabit speeds. It also provides illustrative examples of BER Contour in action, takwith a BERTScope Bit Error Rate Analyzeri .
BER and Eye Diagrams: Why Neither is a Complete Depiction
Most communication links are ultimately judged on their Bit Error Rate (BER) per-formance – how many bits arrive at their destination in error. Like a test at school, a BER tester (BERT) will tell you the link’s test score, whether 9 out of 10, or 1 out of 10. Unfortunately, this doesn’t tell you qualitative information on why that score was achieved, or how to go about getting a better score. For this, people have tradition-ally turned to sampling oscilloscopes to show eye diagrams.

Eye diagrams are an intuitive way of viewing parametric performance. If done correctly, an eye should show every possible pattern combination overlaid, one on top of the other. With all combinations in one place, it becomes easy to see when rise times are too slow, when overshoot is present, or when the eye is being closed due to jitter. So, why not use eye diagrams as the main measurement of link performance?
A big problem comes from the expectations that are set for communica-tions links. Instead of the link being expected to achieve 9 out of 10, or 99 out of 100 (as is the case for some wireless connections), many high speed links are expected to achieve a score of 999,999,999 out of 1,000,000,000 correctly delivered bits (a BER of 1x10-9) or better. Frequently, 1x10-12 is the requirement, although many system vendors are asking their component suppliers to prove their components to 1x10-15 or better.
In order to construct an eye, a sampling scope measures voltage samples. These voltage snapshots differ from measured BER points in a number of important ways.
- First, they grab a small part of any signal at a time, and that small part is only taken at a rate of a few hundred thousand per second. This compares to real data bits flying past at rates of 10 billion per second (for a 10 Gb/s link). This is a very sparse sampling of what is really going on, and makes it extremely unlikely that a sampling oscilloscope will catch the one mistake in 1,000,000,000 bits that is being sought.
- Sampling scopes and BERTs have very different methods of acquiring data – the former has very wide bandwidth but sparse sampling – the latter measures every bit but has a limited input frequency response, more in line with the network equipment that it is emulating. These differences mean that there can be significant result differences between each class of instrument.
A method of viewing link performance that is intuitive, but that contains all of the information needed to judge real link performance would be handy. This is the reason that engineers are increasingly turning to BER contour as a powerful indicator. To understand how a BERT Contour is constructed, it is useful to understand how a BERT gathers information.
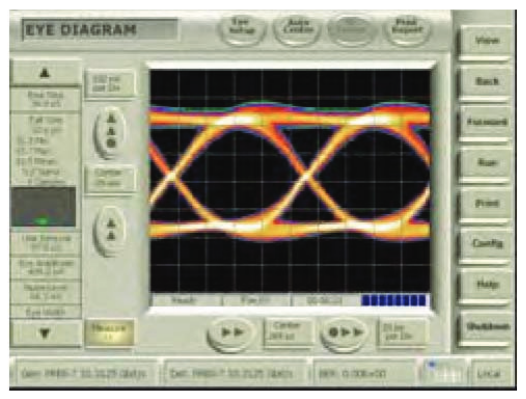
Introducing BER Contour
A BERT Error Detector front-end behaves a lot like a digital receiver in any high-speed communications link – its purpose is to make the correct decision on whether an incoming signal is a one or a zero. To do this, it takes a snapshot at an instant of time. At that instant, the incoming signal is compared to a voltage threshold – which side of the threshold the signal happens to be on dictates whether it is judged a one or a zero. It does this on every single incoming bit, triggered by a clock that is synchronous with the data. Unlike many data receivers, a BERT Error Detector is able to place the decision point very accurately in voltage and time.

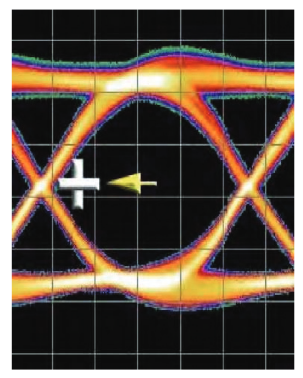
Under normal conditions, a decision point is placed in the middle of the eye, roughly halfway through the bit period, and halfway between the bottom and top voltage rails. This gives the detector the best chance of making the correct decision on each bit.
The picture gets more interesting when the decision point is moved away from this ideal. Imagine a decision point at a voltage half way between the two rails, in the center of the eye. Moving the delay setting between clock and data channels will have the effect of keeping the decision point at the same voltage level, but moving it in time. This looks like the decision point moving left or right within the eye diagram.
A small movement has no effect in this example – the decision point is in an unobstructed region and each decision made is the correct one. It becomes more interesting as the decision point is moved further. As it nears the crossing point of the eye diagram, it still gets the answer right most of the time. However, eventually it will encounter the latest arriving edge – the one edge that is furthest to the right in our example. This edge might have separated from the majority of edges, and be later in time, because it arose from a particular bit pattern combination that was the most difficult for this particular link under test; a runt ‘1’ in a bandwidth-limited system, for example. This one edge means that the decision point sees a voltage level higher than it was expecting to see, and registers it as an error. This is not the normal operating condition of a conventional receiver; instead, it is an artificial condition we have created that allows us to probe the anatomy of that part of the eye diagram.
Moving the decision point further to the left, more late edges will be encountered, and more errors registered. By the time the middle of the crossing point is reached, the incorrect decision is being made a lot of the time. Plotting time on one axis, and errors encountered on the other axis will create a very informative plot. For example, if the first edge encountered is observed frequently and is tightly bunched with all of the other edges, we have a healthy eye that has nothing lurking to catch us out in normal operation. Placing a normal receiver with a decision point in the center of the eye at the end of this link will give us a score better than our 999,999,999 out of 1,000,000,000 correctly interpreted bits. Of more concern is a situation where one edge occasionally is caused to appear very late – late enough to mean that even with the decision point in the middle of the eye, the wrong decision is made. Infrequently occurring events like this are the difference between an unhappy customer returning parts and canceling contracts, and a correctly functioning link. These events occur seldom enough to mean that a sparsely sampled measurement system such as a sampling scope is unlikely to catch them.
The discussion so far has been about moving the decision point in time. This is very useful in probing the jitter performance of a link, and scanning like this is called for in standards such as MJSQii for a test known as Bathtub Jitter or BERTScan

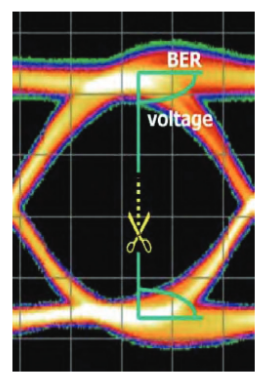
A similar idea can be applied to the vertical (voltage) direction. With the decision point in the center of the eye, keeping the delay setting constant, the threshold voltage is moved. Imagine an example where the threshold is moved up in voltage. Eventually it will reach a point where it encounters the bit that has the lowest one level. This might be a bit that never quite reaches full height before being forced back to zero in the next bit period, and could have arisen because of charge effects in the semiconductor from which the circuit is constructed. Once again, scanning further upwards will cause more ‘low ones’ to be encountered, until most logic ones are falling below the threshold level and are being counted as zeros. We can plot the errors detected against the threshold voltage and produce another slice through the eye that tells us about the health of the system.
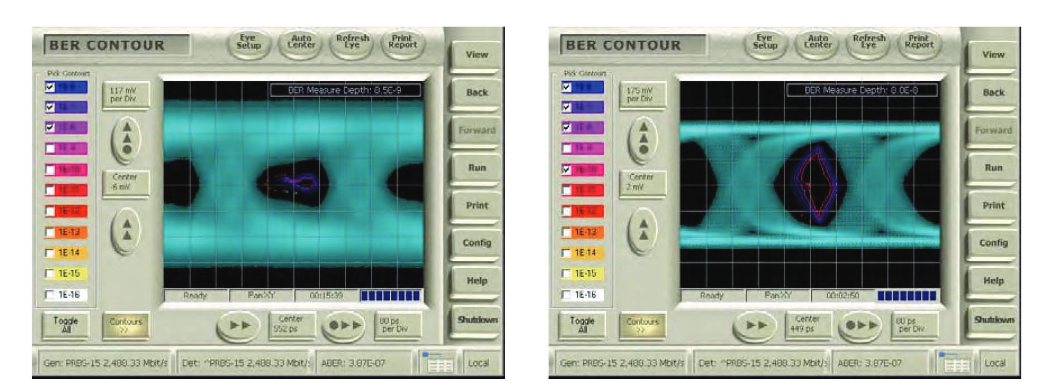
The next logical step is to extend this idea to slices taken at other angles than the two orthogonal ones picked so far. These slices build up a more complete picture of the eye, expressed in BER terms. Taking each curve and finding the 1x10-6 BER point, for example, and joining this point to the other 1x10-6 points obtained from the other curves creates a contour of "iso-BER". In simpler terms, it creates something similar to a topographical map of the eye, where the hills are poor BER and the valleys are good BER.

This view is far more revealing than the two separate simple slices we discussed before. We can now see whether there are lurking problems at any point in the eye, and can see where (if anywhere) we could place a decision point to achieve error-free operation. Notice that the BER contours fall inside the visible representation of the eye in Figure 8. In other words, there are infrequently occurring events that are not visible in a conventional eye diagram that are physically present would limit system performance.
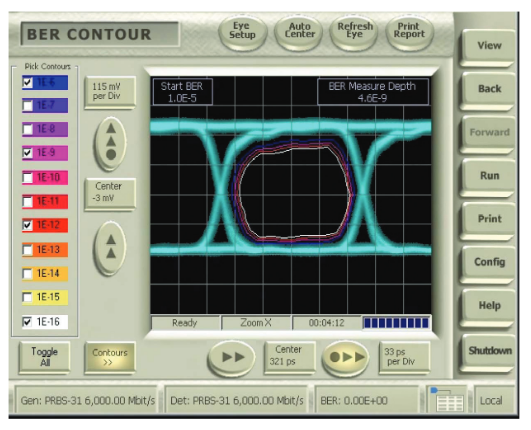
Before discussing some real examples of BER contour, the next section will discuss some of the practical considerations of the Eye Contour measurement.
Considerations
Accuracy and Setting of the Decision Point
Moving a BERT decision point with the exactness and repeatability necessary for an accurate BER contour requires precision. Setting the voltage threshold precisely turns out to be relatively easy with modern components. A harder task is the setting of precision delays. Most high-performance electronic delay line mechanisms are a mixture of fixed sections and variable sections, switched in and out as necessary to achieve the re-quired result. They tend to be complex to control, and non-linear – linear voltage changes do not often give linear changes in delay. There can also be gaps, hysterisis, and changing relationships with temperature and frequency. In commercial instruments, these problems are mitigated by calibrating the delay function, and with calibration, 100-fs steps are reliably and repeatably achievable (not to be confused with claims of 100 fs typical resolution, which gives no information about the accuracy of delay setting). In order to get accurate BER contour results, it is vital that calibration of such small steps is carried out immediately before the measurements are taken.
Detector Input Performance
BERTs are often judged by the quality of their pattern generator output waveform. These have generally become so good that most BERTs in the marketplace have waveform quality far exceeding the performance of the devices that they are intended to stimulate. Of more importance for many of the advanced measurements now possible with modern BERTs is the error detector input performance. This is an instrument quality input, and so should have sufficient bandwidth so that when it is convolved with the device being measured, it does not significantly alter the result. Similarly, the input circuitry should have a well-controlled frequency response and high return loss to faithfully represent and not alter the signal being measured. Carefully designed custom integrated circuits and modules can be created and packaged to offer excellent single-ended and differential performance faithfully representing detector decision circuits.
Speed
- A third consideration is speed of measurement. Traditionally, BER contour has been a very slow measurement to take. There have been two reasons for this: Control of the delay/ voltage threshold has been slow, both because of the use of an external delay line and external computer control, and because of slow responses from the BERT.
- Greatest accuracy of measured points comes from accurately measuring low BER levels. BER levels like 1x10-12 take a long time to measure, as each measurement requires billions of bits. Such measurements can be required multiple times.
Rather than as an after-thought, by knowing the need to quickly reposition decision points in voltage and time and measure even short-segment bit error rates, modern instruments can address the delay control issue very well. For instance, it is possible to reposition a decision point in a few microseconds. This capability, coupled with a fully integrated user interface that automatically determines sampling points and presents the results in an easy-to-view presentation superimposed on the eye diagram, provides for a very fast response.
The second point is more complex, and depends upon the accuracy required. A more-clever approach to the problem of BER contours takes the quicker-to-measure points first, and as the measurement is left to run, gradually fills in the points that take longer. The first points it takes are used to extrapolate what the lower BER contours will look like, and then these predictions are gradually enhanced as more data is taken. Useful information is usually available in less than two minutes. In this way, the longer measurements needed for the deepest BER points are taken when absolutely needed, while intermediate results are immediately available for viewing.
Model
MJSQ is one standard that describes the application of the double-delta, or Dual-Dirac model. This is one way of predicting the behavior of jitter at different points in the eye, and provides simplification of an often complex situation. It does this by differentiating between deterministic components (elements that behave the same way each time they occur; i.e., are bounded) and random components (elements such as noise that are unpredictable at any given instant, and are assumed to obey Gaussian statistics – known as ‘unbounded’). By modeling the two components separately and then adding the behaviors together, it is possible to predict with reasonable accuracy the behavior of the BER/time curve. This was developed for the jitter domain, but has been extended and adapted in the BERTScope to also work in all of the slices used. As is shown in MJSQ Appendix H (January draft), greater accuracy of extrapolation can be achieved by ignoring points higher up the curve in favor of measured points at lower (longer to measure) BERs. The Dual-Dirac model is an approximation, and users wishing to use their own modeling tools are free to export the underlying data and make their own calculations.
What BER Contour Can Show You
Looking in 3-D to visualize eye closure – the "Eye Bowl"
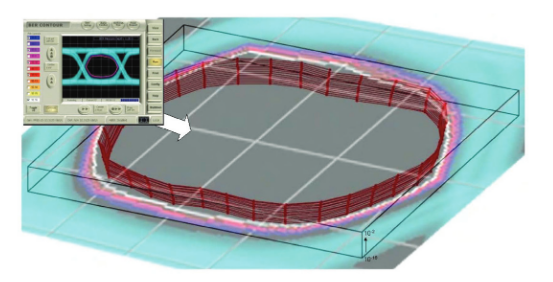
It can be helpful to visualize BER contour in three dimensions to get a feel for what it is showing you. Figure 9 shows a BER contour translated into 3-D to give the idea. The 3-D representation has been dubbed an "Eye Bowl". The Eye Bowl images in Figures 9 and 10 were created by exporting BER Contour data and importing it into a PC-based math program. In Figure 9, the BER contour data has been mapped as a 3-D plot, where the unit cell forms the top dimensions and depth represents BER, with the top face representing approximately 10-2, the bottom face 10-16. A BER contour (light blue) has been superimposed to aid understanding of the transformation that has taken place.

Having made the transformation, it is then easy to see the effect of eye closure. The series in Figure 10 shows systems with steadily worse performance, much of which would be undetectable with a low sample rate eye diagram (although the BERTScope is uniquely equipped with eye diagram capability that allows orders of magnitude more samples to be taken, and so allows more low probability events to be detected).
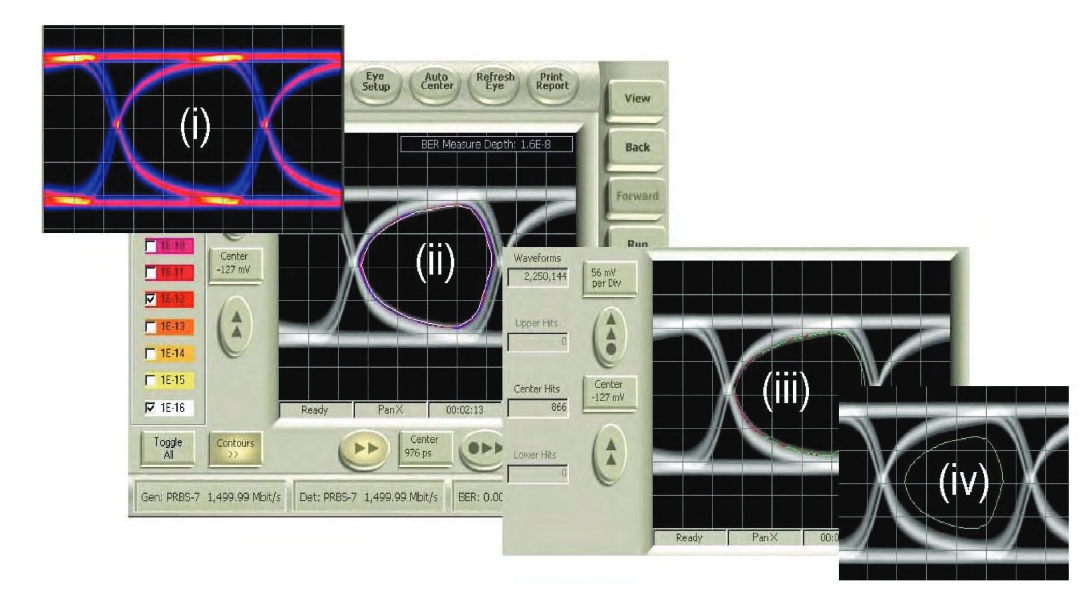
An interesting side-note on BER contour is that the iso-BER contour itself can be used as a benchmark, even in fast manufacturing test applications. By picking one contour line and exporting it as a mask file, it can become a tailored ‘golden performance’ benchmark, used to perform eye mask testing on subsequent devices to monitor process control, quality, etc. Here the BER contour shape is retained, but the measurement becomes a fast voltage sampling (a few seconds) as with conventional mask testing, rather than a slow BER-based measurement. Which contour line picked for export will decide how stringent the test will be, with low-BER (small) contours being easier in the voltage domain than higherror (larger) contours. The sequence is shown in Figure 11.
Examples of BER Contours
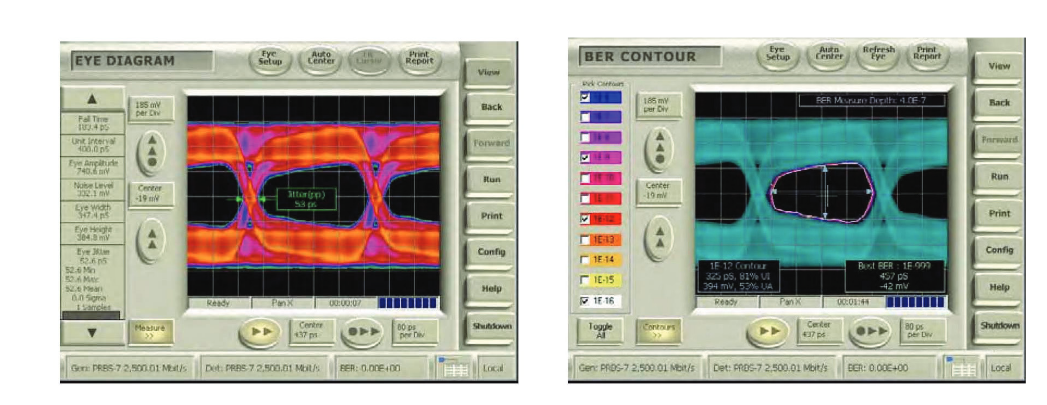
BER Contour is an excellent way of revealing the true performance of a system. For example, eye diagrams that may appear to be severely degraded may have imperfections caused by mechanisms that are entirely deterministic, with a high probability of occurrence – or more simply put, what you see is what you get, and there is nothing lurking at low probability levels that will cause system problems. The flipside is also true; some eye diagrams that seem almost textbook in their openness can have lurking problems deriving from unbounded mechanisms. These cases are illustrated in Figures 12 and 13, respectively.

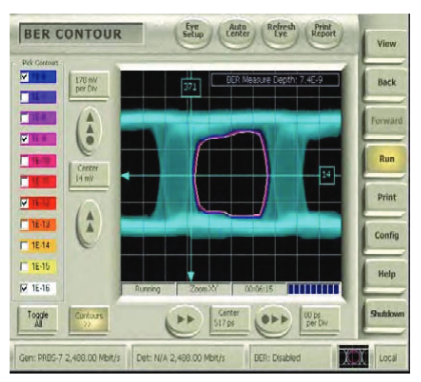
Construction of 'stressed eye' jitter tolerance measurements also provides some good examples of particular BER Contour impairments. In the following figures (Figures 14-17), a BERTScope pattern generator has been impaired in different ways.


Conclusion
BER Contour provides a revealing view of system parametric performance that is intuitive and comprehensive. With recent advances in instrument technology, it is also now fast and accurate, making it a practical proposition in development, troubleshooting, and verification environments. It can also be valuable in benchmarking golden devices in manufacturing.

