Abstract
Jitter Map is a capability on the BERTScope that uses BER measurements tomeasure Total Jitter as well as decompose jitter beyond basic Random and Deterministic Jitter. This paper introduces the reader to the methodologies used in this innovative tool, and explains novel features which allow users to delve into jitter problems in new ways, such as examining Random Jitter on each edge of the data pattern, separating out the jitter caused by transmitter pre-emphasis, and performing jitter decomposition on long patterns such as PRBS-31.
Introduction
Based on the inherent statistical depth observed by real-time bit error ratio (BER) detectors, the accurate measurement of jitter using BER Testers (BERTs) is well recognized[i]. Popular measurements of Total Jitter (TJ), dual-Dirac Deterministic Jitter (DDδδ) and dual- Dirac Random Jitter (RJδδ) can be found on just about any BERT. At the same time, more sophisticated jitter separation techniques have been developed on oscilloscopes to provide designers with insight into the various sub-components of jitter. What's missing is a direct connection between sophisticated jitter component analysis and the confidence of deep, BER-based total jitter measurements.
The BERTScope now bridges this gap. Jitter Map features allow comprehensive jitter decomposition especially designed for the bit decision world of digital communications applications. Built on top of the fundamental depth of measurement expected from a BERT, this new capability is also enabled by the precision low-jitter time base, adjustable decision circuit sampling, as well as the pattern and subrate synchronization of a BERTScope.
Measurement Engines
Studying jitter in digital communications systems is the study of edge transition timings as they are presented to a bit decision circuit. The early or late behavior of edge transitions with respect to ideal timing is, in fact, jitter. An edge transition that comes too late or too early can cause the wrong bit decision to be made and, thus, a bit error. Furthermore, in the world of digital communications applications, jitter on some edges ends up being more important to bit error ratio than jitter on other edges – as some edges are at the extremes of the total jitter population.
It is important in any method of jitter analysis to understand the intrinsic measurement physics to be able to assess where inaccuracies might creep in or where measurement efficiencies might exist. In popular equivalent-time sampling scopes, for instance, one might wait 25 μsec to capture a precise voltage of the signal under test at a precise time offset away from a trigger point. When studying jitter in digital communications systems, efficiency could be gained by instructing the sampler to only sample at time offsets that should report voltages very near the decision threshold voltage. With these nearby voltage readings and by cleverly characterizing the typical slopes of families of edges, estimates of the time when the edge would have crossed the threshold can be computed. At these rates and with this optimization, a popular sampling oscilloscope can measure 40,000 edges in a second.
In a 'real-time' oscilloscope, an internal sampling frequency is synthesized to create a nominally-consistent sampling time between fast analog-to-digital conversions of the signal under test. Typically, multiple channels of analog-to-digital converters are interleaved. While this inherently introduces possible time and amplitude error in the interleave process, this is done to achieve the highest sampling rates. These samples are contiguous in time and therefore represent the continuous signal-under-test. For example, at 40 G sample/sec, sample intervals would be nominally 25 picoseconds, which would also be the amount of uncertainty where interpolation would be required to estimate exactly when a bit crosses the logic threshold. These samples are used to reconstruct the waveform using some form of interpolation. Doing this to sub-picosecond accuracy is certainly a challenge. In a given 25 μsec, 1 million samples can be sent to a memory which, at 10 Gbps might represent some 250,000 bits. Software processing is then done to calibrate and reconstruct the waveform to be able to determine the time of each transition. If this software processing were to only take 6 or 7 seconds for a million samples, an effective edge time sampling rate that matches popular sampling scopes is achieved.
Before studying what a decision-circuit based measuring system would do in this case, it is important to revisit why these edge timing measurements are being made. Jitter for a digital communication system is defined in terms of what bit error ratio it causes. Fundamentally, bit error ratio is a cumulative probability function. That is, at a given sampling time, bit errors are the integral of all individual edges in error. This is a very important distinction because it means that in order to determine a cumulative probability using edge-timings from waveforms as the fundamental measurement, one must time a large number of edges and use software to accumulate the offending edges (thresholded by where the edge time lands too early or too late for the desired measurement instant). Alternatively, a BERT's bit decision circuit with its sampling time set to the same measurement time threshold will accumulate a count of all offending edges in real-time. In our example 10 Gbps system, in 25 μsec 250,000 bits can be counted. In one second, 10 Billion bits can be counted.
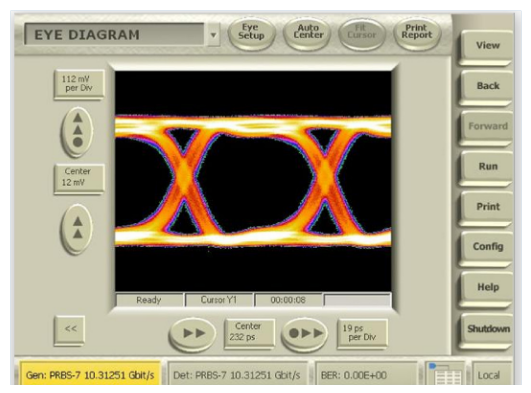
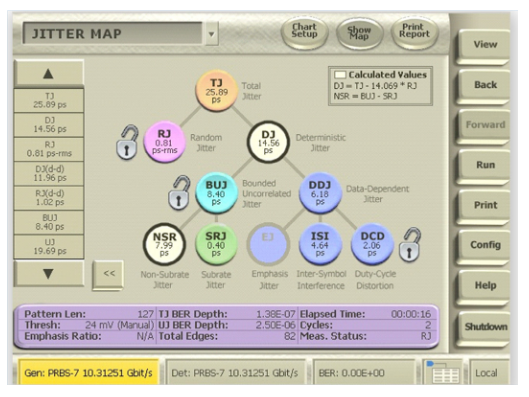
BERTScope Jitter Map
BERTScope Jitter Map is a new kind of jitter analysis engine. It has the ability to not only measure deep cumulative probability density functions, but it can also selectively do this for individual edges of data patterns and collections of edges. It does this by using a pattern trigger, as has been key to jitter decomposition measurements by common sampling scopes. In addition, the BERTScope's error location analysis quickly enables the determination of which data bits contribute to bit errors. In the following sections, we are going to look at each of the jitter sub-components, and examine the way that Jitter Map is able to produce fast, accurate and repeatable jitter results. We will follow a single example using a signal at 10.3125 Gb/s, PRBS-7 data pattern, with some added random and sinusoidal jitter and duty cycle distortion.
The top level summary screen is an intuitive jitter tree, as shown below. More detail is available by touching subcomponents that have '3D' buttons.
Total Jitter (TJ) Measurement
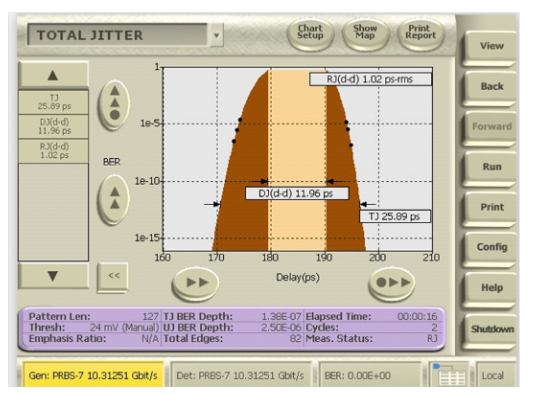
Perhaps the most important jitter measurement is Total Jitter (TJ). It is also the most time consuming to measure. Total Jitter requires measuring the available eye opening typically to a point where a BER of 1x10-12 is found1 . Bit error ratio (BER) is computed as the number of errors divided by the number of bits transmitted. Because of this, confidence in the measurement increases as the number of errors increases. It is not sufficient to only look at 1x1012 bits to measure a 1x10-12 BER. It is commonplace to require enough bits to observe 10 or 100 errors to be confident. This means that making a single 1x10-12 BER measurement in a 10 Gbps system would take 16-160 minutes (naturally, this scales linearly with data rate). While it is very possible to wait this amount of time to get a completely measured BER value, most BER-based TJ measurement methods also include initial extrapolation methods to use more shallow BER measurements to predict the 1x10-12 opening. This is done in the Jitter Map solution.
In this view, Jitter Map shows the results of both the direct measurements and the extrapolation down to the 1x10-12 point. The extrapolation method makes a smooth curve out of the measured BER values. Here, the y-axis is plotted as the LOG10 of the BER values. Mathematically, the LOG10 of the inverse of the cumulative Gaussian distribution is nearly identical to a parabola for values farther than a few standard deviations away from the mean. Utilizing this observation, extrapolation for a good TJ measurement is easily accomplished from BER values. Further, fundamentally, these extrapolation techniques are required for all TJ measurement methods (unless you want to wait for a complete measurement) so the amount of error in a given method depends on how far of a reach is needed for the extrapolation to give a 1x10-12 value. BERTScope measurements taken in a few seconds can easily show confident levels of BER 1x10-8 and 1x10-9 by inspecting billions of bits, while oscilloscope methods might inspect only 100,000 bits, thus only giving confidence to higher than 1x10-5 BER levels. Much less extrapolation is needed in the BER-based measurement method.
While performing the Total Jitter analysis, Jitter Map also uses the measured BER values to compute the popular dual-Dirac values for Random Jitter and Deterministic Jitter, RJδδ and DJδδ. The dual-Dirac model was an early form of jitter component separation and it holds perfectly well today for applications where DJ can be modeled as two like Dirac functions. Realistically, though, this is not a common form of jitter distribution. The dual-Dirac method for jitter separation becomes less precise when the distribution of jitter in the areas of measurement interest do not follow the same Gaussian distribution as a single bit might truly have. This is because the overall transition location probability distribution near the extremes of the eye opening is actually formed as a composite of many closely spaced edges in the pattern and because the real shape of the probability distribution is typically caused by jitters other than random ones (e.g., sinusoidal jitter, etc.). While the dual-Dirac methodology continues to provide a convenient relative jitter performance metric, from a high-level point of view, it becomes less reliable for signals that have long patterns or non-random jitter components.
Just as in the dual-Dirac model case, the first break-down for new jitter decomposition analysis is to also separate out jitter that is random from jitter that is deterministic.
Random Jitter (RJ) Measurement
Random jitter is very difficult to measure. In addition, RJ has a different interpretation in a digital communications systems than, say, random components of a phase noise analysis might have for a frequency synthesizer. This is because digital communications systems are concerned with the effect of RJ resulting bit errors. RJ on bits that don't contribute to bit errors is not seen by digital communications systems. Further, only the RJ on bits that do contribute bit errors set the overall impact of RJ in the system.
Random variations of edge timing which cause bit errors about a bit decision point are the result of the combination of a number of random processes. The method by which these processes combine (addition, multiplication, attenuation) and the way this combination works with other deterministic or even non-linear phenomenon drive the overall RJ. The result is that one bit of a data pattern can have a different random jitter component than another.
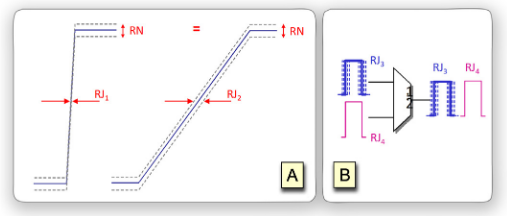
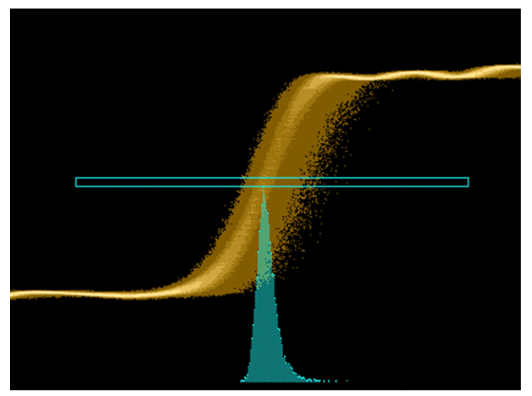
This may not be a well known idea, but it is simple to demonstrate. Consider a real signal that passes through a decision threshold at different slopes depending on the bit pattern. In this signal, the voltage noise present in the vertical axis will translate to different amounts of time-domain RJ depending on the slope ((A) in the figure above). As another example, consider a combinational gate used as a multiplexer to output interleaved data bits from two sources that have different RJ. In this example, the output stream would have one jitter for even bits and another jitter for odd bits ((B) in Figure 4).
It is also observable that the resulting distribution from combining multiple effects of RJ can have an unequal distribution about the mean i.e. different RJ on the left-hand side of the edge than the righthand side of the edge. From a digital communication system's point of view, this becomes a very important characteristic as bit errors are always the result of approaching the eye crossings from either the left or the right. This would not be observed, for example, in a phase noise type measurement, which typically results in a jitter frequency spectrum from which only an overall average RJ measurement can be obtained without any information on the shape of the jitter distribution.
It is also observable that the resulting distribution from combining multiple effects of RJ can have an unequal distribution about the mean i.e. different RJ on the left-hand side of the edge than the righthand side of the edge. From a digital communication system's point of view, this becomes a very important characteristic as bit errors are always the result of approaching the eye crossings from either the left or the right. This would not be observed, for example, in a phase noise type measurement, which typically results in a jitter frequency spectrum from which only an overall average RJ measurement can be obtained without any information on the shape of the jitter distribution.
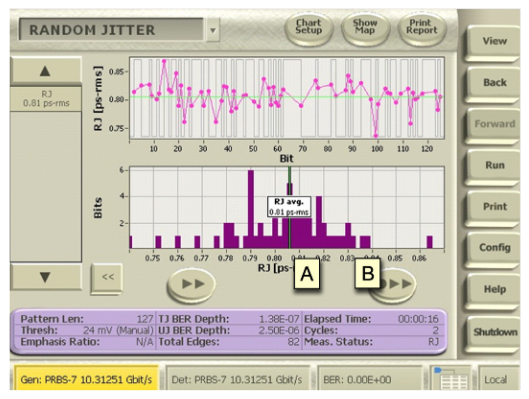
Jitter Map RJ measurement is a two-step process:
- First, the tails of the cumulative probability density function of a single edge of the pattern are measured, which has the effect of removing all data dependent jitter from the measurement. This measurement includes other non pattern dependent jitter like Bounded Uncorrelated Jitter (BUJ). However, these BUJ components appear as a deterministic component and do not fit the shape of an error function for a random signal on either extremes of the distribution. Thus, dual-Dirac RJ/DJ separation is used to determine the RJ value for this deeply measured single bit at this step.
- In the next step, remaining bits of the data pattern are studied (with initial emphasis placed on bits that land on the left-most or right-most side of the overall distribution). These bits can be studied quickly as the desired outcome is to generally gauge variations in overall jitter from one bit of the pattern to the next and to compare it to the deeplymeasured single edge. An overall average RJ number is computed based on the average of RJ from all edges while the individual RJ numbers are displayed for added diagnostic information.
Bounded Uncorrelated Jitter (BUJ) Measurement
Non-random jitter that does not correlate with the data pattern is called Bounded Uncorrelated Jitter (BUJ). This jitter includes components such as harmonically-related subrate jitter or other periodic jitters as well as crosstalk. Measuring BUJ is done using the same measurement data as used for the RJ measurement described above. The cumulative probability distribution of a single edge of the data pattern is deeply studied and random components of jitter separated out to leave the BUJ amplitude using the dual-Dirac model.
One well-known shortcoming of the dual-Dirac method of separation of deterministic and random components is that it sometimes mistakes deterministic jitter that looks Gaussian at high probabilities as random jitter. This is also caused by Data Dependent Jitter (DDJ) from long patterns, which can take on a truncated Gaussian shape. However, when studying a single edge of the data pattern, all DDJ is excluded from the measurement, circumventing this problem altogether.
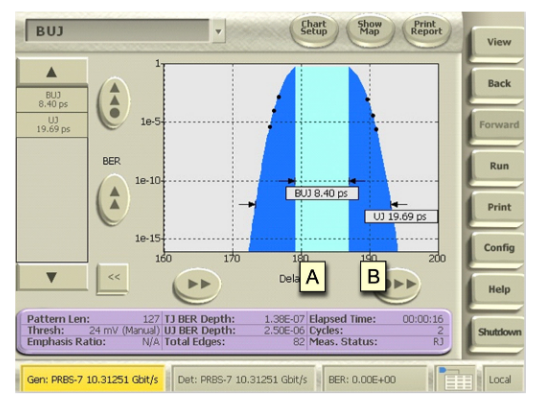
Yet error in BUJ/RJ separation may still occur when the shape of the BUJ distribution does not fit the dual-Dirac model of an RJ distribution convolved with extreme edges down at the levels of BER where it is measured. For instance, sinusoidal jitter has a distinctive jitter shape that steepens the walls of composite jitter distributions. To reduce this error, the BUJ measurement uses BER points that are deep enough to avoid the high probability area of the distribution that can throw off the dual-Dirac model. While the BER points in the above plot may seem relatively shallow for a BERT, one must remember that this is being performed on a single edge of the data pattern, and thus, not only is the problem of long pattern DDJ masquerading as RJ (discussed previously) avoided, but the depth shown is relatively deep compared to the depth one may reach with oscilloscopes in the same amount of time. This measurement is continually deepened as Jitter Map runs longer.
Data Dependent Jitter (DDJ), Inter-Symbol Interference (ISI), and Duty Cycle Distortion (DCD) Measurements
Data Dependent Jitter, Inter-Symbol Interference and Duty Cycle Distortion are types of jitter that depend directly on the data pattern. Measuring each of these requires knowing where rising or falling edges occur on either extreme of the overall eye crossing. One way of getting the data for this measurement is to find the average transition time of every bit in the data pattern. Plotting these average edge timings on a histogram facilitates the measurement and produces an intuitive view of DDJ, ISI, and DCD.
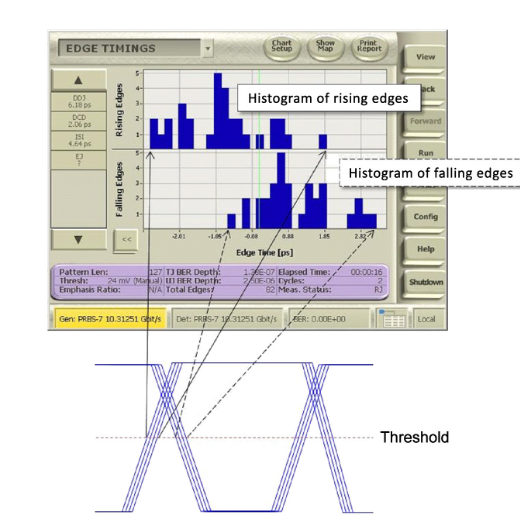
With this data, DDJ is the overall width of the rising and falling histograms combined, or in other words, the time difference between the earliest and latest edge. The DCD is determined by the time difference between the average of the rising edge times compared to the average of the falling edge times. The ISI is determined as the width of the rising or falling edges histogram, whichever is larger.
For short patterns, this is easily accomplished quickly; however, for longer patterns, it becomes impractical to accurately determine the average time of all edges in the pattern in a reasonable amount of time. Alternatively, though, because the goal of the measurement is to determine the widths and centers of averaged rising and falling edge distributions, accurate estimates of DDJ, ISI, and DCD measurements can be made by visiting edges that land at the extremes of these distributions along with a far smaller number of randomly selected edges.
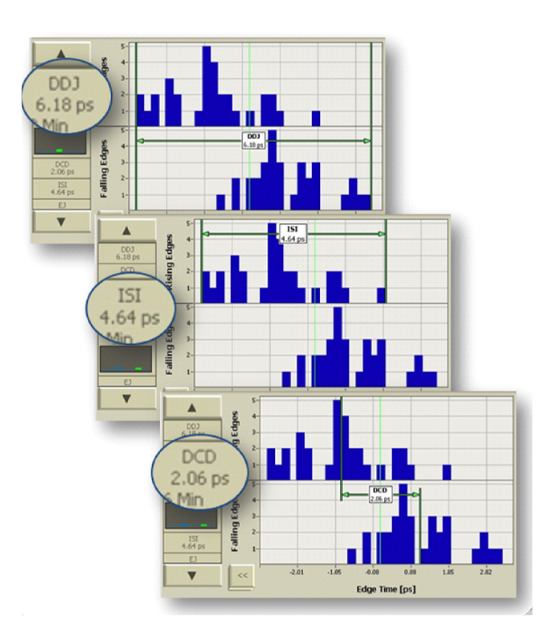
In order for Jitter Map to identify the edges to include in these measurements, the unique BERTScope feature of Error Location Analysis (ELA) is used[iii]. In ELA, errors are analyzed by their location within the bit stream. This error data can be analyzed to show how bit errors correlate to the user pattern—Pattern Sensitivity Analysis. Bit edges that are found to cause errors at the extremes of the eye opening are prioritized for this analysis. By visiting as few as 100 edges, accurate estimates of DDJ, ISI, and DCD can be determined in any length data pattern. Over time, Jitter Map includes more edges in this analysis and then re-measures edges to increase precision.
Deterministic Jitter (DJ)
The Deterministic Jitter (DJ) reported in Jitter Map is a calculated peakpeak measurement and is reported as the sum of BUJ and DDJ. It is shown as an estimated peakpeak measurement due to the fact that it is the result of the summation of a dual-Dirac measurement (BUJ) with a peakpeak measurement (DDJ).
Subrate Jitter (SRJ) Measurement
Often, Deterministic Jitter is induced into systems due to processing in nearby logic. Interactions like these cause jitter that could be synchronous or asynchronous and would fall into the category of BUJ (“Uncorrelated” due to jitter not being correlated to the data pattern). Clock-synchronous jitter is a special and typical case of this type of jitter. Signal processing such as mux/demux, channel coding, block formatting and lower-speed parallel processing all have the potential of shifting edges at integer number of clock boundaries.
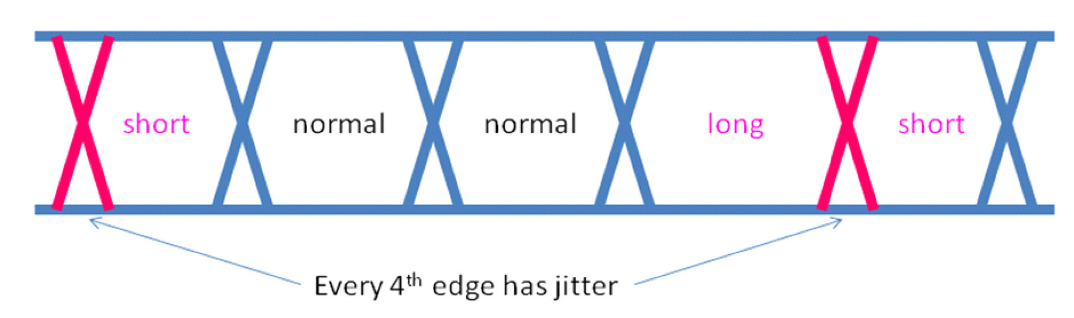
For example, a 4:1 mux stage on a transmitter might advance or retard the timing of edges that occur at the same time as the internal divide-by-four clock parallel-loads all registers. If one were to look at four eye diagrams triggered by a onequarter rate clock, they would see two eyes with the nominal eye width and one short and one long eye width surrounding the jittered edge. This would not be interpreted as ISI as it would be observed on all bits of the pattern (as long as the pattern length is not a multiple of four).
The BERTScope is equipped to collect statistics about cumulative edge probabilities at programmable divide ratios. It does this for all transitions within each divide ratio to determine the average transition for all eyes that make up a given divide ratio. Any non-harmonically related dissimilarity between the average transition times for all eyes that make up a given divide ratio is deterministic jitter that correlates to that divide ratio and is reported as Subrate Jitter (SRJ). Any BUJ that is larger than the SRJ number is further termed the Non-Subrate Jitter (NSR).
Care must be taken to not confuse Subrate Jitter with pattern-dependent ISI. If the data pattern under test is a perfect multiple of a subrate divider, then the jitter found for that subrate is not included in the SRJ number as it will be correctly identified as a component of ISI.
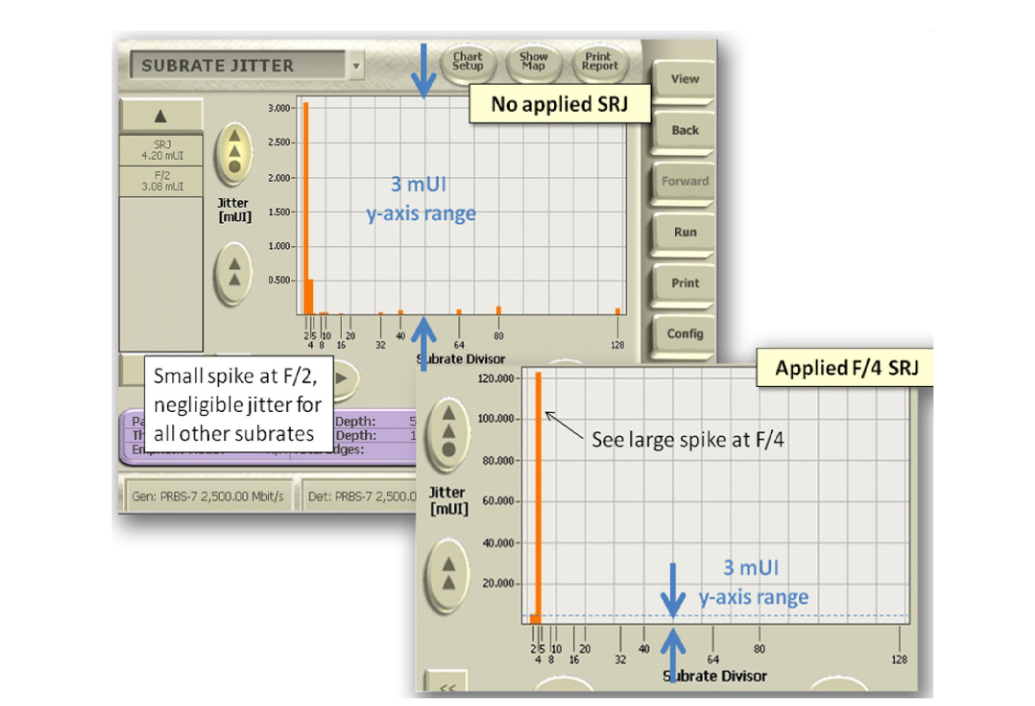
Default Subrate Jitter divide ratios studied in Jitter Map include 2, 4, 5, 8, 10, 16, 20, 32, 40, 64 and 128.
Emphasis Jitter (EJ) Measurement
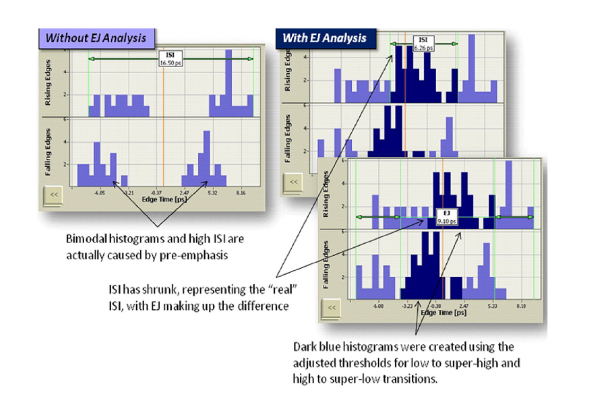
Modern systems utilize transmitter emphasis (boosting of higher frequencies of the signal) in order to combat frequencydependent losses of cables, backplanes and channels of all types. Adding transmitter emphasis causes pattern-dependent edge timing shifts which would normally be interpreted as added ISI. Because jitter caused by emphasis is a “good” form of jitter, it is helpful to be able to distinguish which datadependent jitter is due to emphasis and which is due to ISI.
Now, let us add transmitter pre-emphasis to our example signal. The result is shown below in the eye diagram. All other stresses have been removed to draw a clearer eye diagram that demonstrates jitter due to pre-emphasis.
Jitter that is due to transmitter emphasis is referred to as Emphasis Jitter (EJ). Jitter Map quantifies EJ by analyzing the timing of edges that have emphasis applied to them separately from the edges that don't.

When thinking about a two-tap emphasized signal, it is helpful to think of the regular logic voltage levels as the high-level or low-level and the emphasized levels as super-high or super-low. In emphasized signals, transitions can only occur between low to super-high, high to super-low and superhigh to superlow. To study the jitter in these transition cases, different logic thresholds representing the midpoints of the known level-change type need to be used as the bit decision threshold. The vertical middle of the eye is used as the threshold for super-low to super-high and super-high to super-low transitions. Low to super-high transitions must use a higher threshold and high to super-low signals must use a lower threshold. The amount of change in the threshold level (up or down) depends on the emphasis ratio. In Jitter Map, the emphasis ratio (in dB) can either be automatically determined or manually entered.
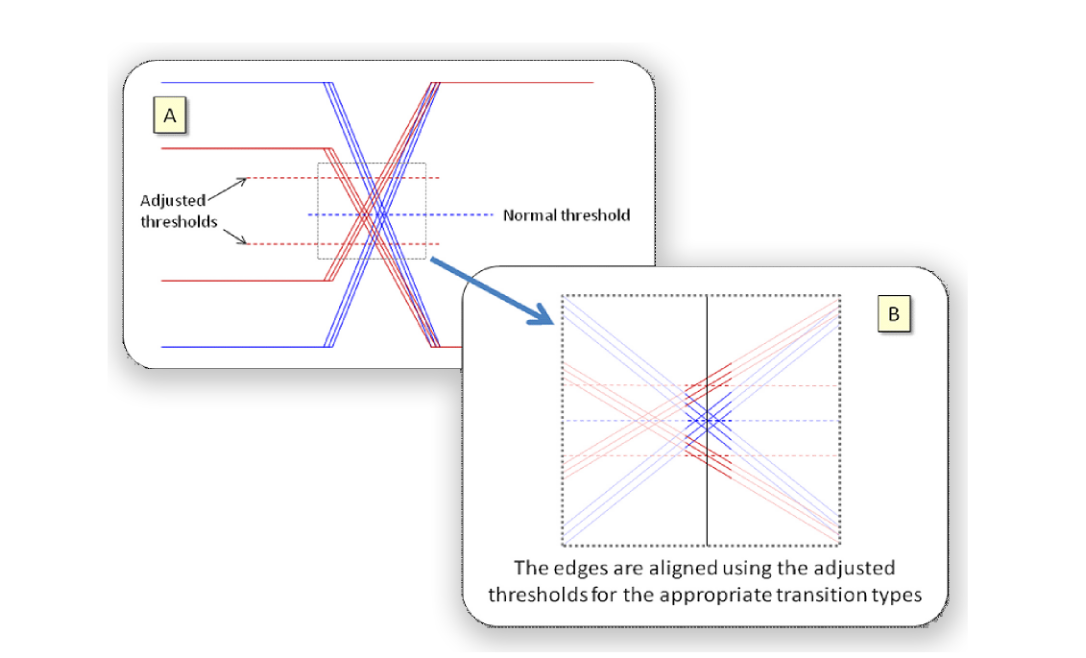
When emphasis analysis is performed, DDJ histograms are created using the normal threshold level as well as the adjusted threshold levels (see Figure 14). ISI is measured on the histograms using the adjusted threshold levels, and EJ is the difference in DDJ from the histograms using the normal threshold and those using the adjusted threshold. In this way, it is possible to see how much “real” ISI is present even in an emphasized signal. Any ISI that is registered is the result of non-ideal emphasis and is rightly reported as residual ISI.
Long Pattern Jitter Triangulation Using Pattern Lock
Very long patterns present a problem to any jitter decomposition method. Inherently, the pattern repetition rate becomes so slow, that required measurements triggered by the pattern repetition are unable to collect enough information in any reasonable amount of time. A typical example of this happens when PRBS-31 data patterns are used. Even in the case of 10 Gb/s signals, the repetition rate of the PRBS-31 data is 4.6 Hz.
At the same time, the expected general behavior of jitter measurements from switching between a nominal test pattern and a very long test pattern is only a change in the ISI. This would assume that changing the data pattern type would have little or no effect on the residual Random Jitter (RJ), the Duty Cycle Distortion (DCD) and the Bounded Uncorrelated Jitter (BUJ). By making this assumption, Jitter Map allows users to lock-down the results of a jitter analysis on a shorter pattern and uses this information along with a deep Total Jitter (TJ) measurement of all edges in the long pattern to triangulate and report the expected jitter decomposition for the longer pattern signal.
In Long Pattern Lock Mode, Jitter Map performs the following calculations after the RJ, DCD, and BUJ values have been locked down using a short, synchronized data pattern:
- 1. Since Jitter Map assumes that the change in jitter from a short to long pattern is a change in ISI, the ISI for a long pattern can be approximated by the change in TJ from a short to long pattern.
- 2. From this, DDJ is approximated by the sum of ISI, which has just been calculated in the previous step, and DCD, which has been locked down based on a shorter data pattern.
- 3. Finally DJ is approximated by the sum of DDJ per the previous step and BUJ, which is also locked down using a shorter data pattern.
Conclusion
The new Jitter Map feature in the BERTScope combines the algorithmic benefits of measuring real-time cumulative probability distributions with outstanding timing and decisionmaking fidelity to decompose jitter into its components. New jitter components, such as jitter due to intended pre-emphasis extend the state-of-the-art of jitter decomposition. Jitter Map analysis relies on the BERTScope's error location analysis to create fast and accurate estimates reducing the need to measure all edges in a data pattern. Finally, by locking down jitter results from a shorter pattern and combining this with deep measurements of the entire pattern, jitter separation estimates can be made on very long patterns such as PRBS-31.

