Keys for Successful Coherent Acquisition

As demand for data increases, network operators continue to search for methods to increase data throughput of existing optical networks. To achieve 100Gb/s, 400Gb/s, 1Tb/s and beyond, complex modulation formats have become prevalent. These modulation formats present new challenges for the designer when it comes to choices of test equipment.

The typical test and measurement coherent optical acquisition system consists of three major building blocks: the coherent receiver, a digitizer - typically an oscilloscope – and some form of algorithmic processing. Certain performance parameters such as the coherent receiver bandwidth or oscilloscope sample rate have an obvious impact on the measured signal quality. However, there are a number of other aspects to the choice of a coherent optical acquisition system that may be less obvious but can play an equally key role in a successful test system.

This technical brief will examine three such aspects in further detail and show how they can play a vital role in a coherent optical test system. These are:

1. Optimal Error Vector Magnitude (EVM) floor and oscilloscope digitizer effectiveness;
2. Future-proofing the system for next generation communications technology;
3. Analysis techniques for conclusive evaluation.

Achieving Low EVM

Low EVM and Bit Error Ratio (BER) are basic requirements for any coherent optical acquisition system. There are a wide range of system impairments and configurations issues that can affect the final optical EVM.

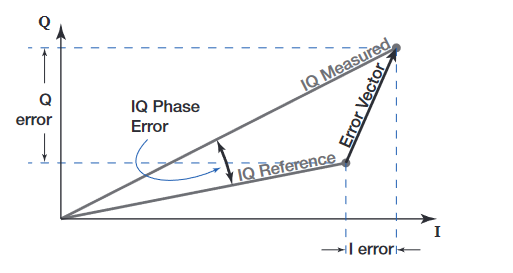
Within the Optical Modulation Analyzer (OMA) - the receiver - EVM can be impacted by a number of receiver issues such as: IQ phase angle errors, IQ gain imbalance, IQ skew errors, and XY polarization skew errors. The good news about these types of errors is that they can be precisely measured and their impacts calibrated out in the algorithmic processing that typically follows coherent detection. Receivers such as the OM4000 Series Optical Modulation Analyzers are tested at the time of manufacture. A unique calibration file is created and used by the optical modulation analyzer software to remove the impacts referenced here.

In some cases the optical receiver has been built from scratch in the engineer's laboratory but it is still desired to be used as a test instrument. In these circumstances an OM2210 Coherent Receiver Calibration Source can be used to measure key performance parameters of this uncalibrated, "home-built" receiver and create the same calibration files. Ultimately, the primary impacts of the OMA on EVM measurements can be corrected.

Once the signal is received; the next step is digitization on the electrical signal paths by a multi-channel oscilloscope. With the oscilloscope, a number of instrument factors affect EVM, the most fundamental being oscilloscope bandwidth and sample rate. Most engineers testing 100G coherent optical signals use 4-channel oscilloscopes with bandwidth in the 23 GHz to 33 GHz range and sample rates in the range of 50 GS/s to 100 GS/s. 400G system evaluation requires oscilloscopes with 70 GHz bandwidth at 200 GS/s sample rates.

Assuming an oscilloscope with appropriate bandwidth and sample rate is utilized, and all OMA impairments are being corrected algorithmically, the lowest measurable EVM comes down to a function of the effective number of bits (ENOB) of the oscilloscope.

EVM Definition

Error Vector Magnitude (EVM) was recently defined by the IEC in IEC/TR 61282 101.In this Technical Report (TR), EVM is defined as follows.

The error vector is simply the vector that points from the actual measured symbol to where that symbol was intended in the signal constellation diagram. The 'reference' or intended symbol location is defined by the modulation type except for the overall signal magnitude. For a group of symbols, the reference magnitude is taken to be that which results in the lowest EVM for the group. Once this magnitude is determined, both the signal and the reference symbols are divided by the magnitude of the largest reference symbol to normalize the data according to Section 4 of the TR.

Normalizing the data in this way has the effect of presenting EVM as a fraction of the largest reference symbol magnitude. This makes comparisons between QPSK and QAM EVM more difficult. Wireless standards have chosen to use square root average symbol power for the normalizing factor. It may be that the optical standard will change to this method over time. The OM4000 software allows the normalizing factor to be customized for this reason. The default definition follows the TR.

These considerations provide the following formula for EVM when expressed as a percent:

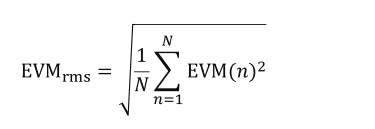
Where EVM(n) is the normalized error-vector magnitude of each symbol and N is the number of symbols in the group. As stated above, the TR assumes normalization by the largest reference symbol.

This definition is now well established, but there are a number of experimental factors in addition to the normalization method that need to be specified for the EVM measurement to be meaningful. These include:

1. Measurement bandwidth
2. Signal filtering
3. Phase tracking bandwidth

The OM4000 Series software uses phase tracking by default.A filter is applied to the phase data to reduce the effects of noise on the displayed modulation phase. The optimum digital filter has been shown to be of the form (1−α) (1+αz−1)⁄, where α is related to the time constant, τ, of the filter by the relation τ = –T/ln(α), where T is the time between symbols2. So, an α = 0.8 when the baud rate is 2.5 GBaud gives a time constant τ = 1.8 ns or a phase-tracking bandwidth 12πτ of 90 MHz

EVM Accuracy and Reproducibility

There are several factors that limit EVM accuracy and reproducibility. These can be generally categorized as systematic or random noise contributions. Systematic error is primarily a function of coherent receiver imperfections. Receiver imperfections include I-Q phase error, I-Q amplitude mismatch, skew, cross-talk, and frequency response. These errors are corrected in data post-processing, but a residual error remains since there will be some uncertainty in measurement of the imperfections.

The random EVM noise contribution is the input-referred rms noise divided by the largest symbol magnitude. Increasing the signal power thereby reduces this random-noise contribution until the digitizer dynamic range limit is reached. Digitizer instantaneous dynamic range is usually measured by effective number of bits or ENOB which is the number of bits required for an ideal digitizer to have the same noise level as the actual digitizer. By convention,

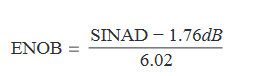
where,

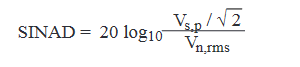
is Signal-to-Noise-and-Distortion in dB, V_s,p is the peak voltage of the full-scale signal, and V_n,rms is the rms noise and distortion.

Putting it another way,

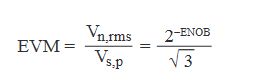
This sets the ultimate limit on EVM noise level at 2−ENOB/√3 when the input signal exactly fills the digitizer dynamic range. Digitizer ENOB can usually be improved with a digital lowpass filter if the entire digitizer bandwidth is not required. Low ENOB, then, is key to achieving the lowest possible EVM.

Asynchronous Time Interleaving

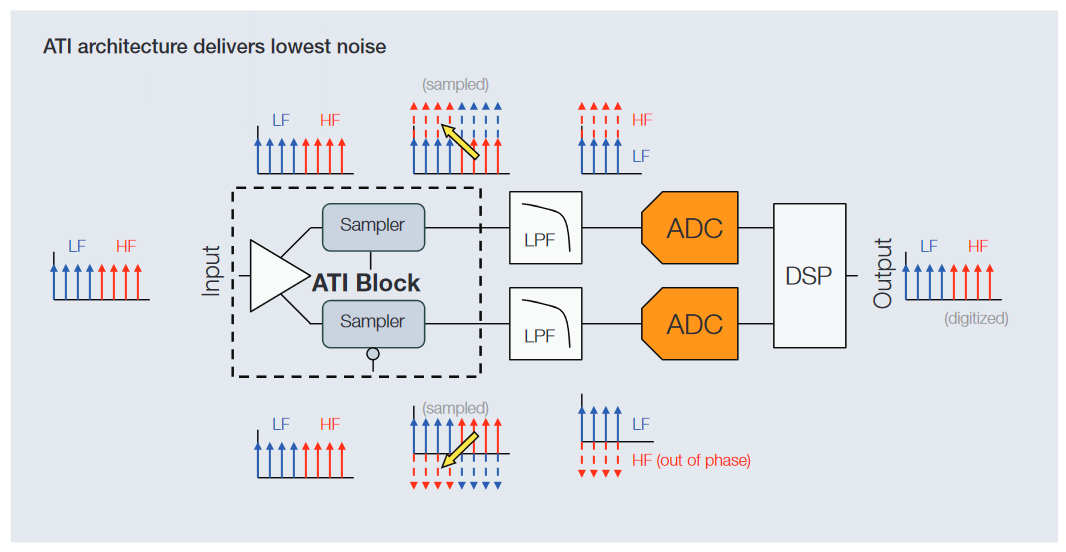
Interleaving is not a new technology in oscilloscopes. As soon as the bandwidth requirements extend beyond the sample rate capability of the commercially available analog-to-digital converter (ADC) components, it becomes necessary to find other techniques to utilize available components to meet those extended requirements, or design a new generation ADC. Both LeCroy and Keysight deploy in their oscilloscopes frequency interleaving techniques that extend bandwidth, but do so at the cost of increased noise in the measurement channel. For many applications, the degraded signal fidelity provided by frequency interleaving is problematic, and as a consequence, Tektronix has chosen to take a different approach.

The limitation of the frequency interleaving approaches lies in how the various frequency ranges are added together to reconstruct the final waveform, a step which compromises noise performance. In traditional frequency interleaving, each ADC in the signal acquisition system only sees part of the input spectrum. With Tektronix' patented ATI technology, all ADCs see the full spectrum with full signal path symmetry. This offers the bandwidth performance gains available from interleaved architectures while preserving signal fidelity and ensuring the highest possible ENOB.

To learn more about this exciting innovation, download the white paper Techniques for Extending Real-Time Oscilloscope Bandwidth from www.tektronix.com

Future Proof for Next Generation 400G and 1Tb Testing

While the bulk of coherent optical R&D activity is currently focused on 100G, research and development of 400G is already underway at many sites. Most major test instruments purchased are expected to be directly useful for many years. Even customers that are not currently testing 400G will likely need to within the lifetime of their 100G test instruments. Purchasing a system that is the right performance and price for 100G now, but still allow expansion into 400G in the future, is a key system purchase requirement.

Customers testing 100G signals commonly employ 4 channels of 33GHz real-time oscilloscope acquisition. Depending on choices of baud rate and modulation formats, testing 400G typically demands oscilloscope bandwidths greater than 65 GHz. But acquiring a full dual-polarization system at 65 GHz may be outside of the budget of many labs that only need to test 100G today.

The Tektronix DPO70000SX Series real-time oscilloscopes allows customers to purchase what they need for 100G testing today and still retain full value of those instruments when the need for 400G testing arrives. The DPS77004SX oscilloscope system offers four channels of 33 GHz acquisition distributed across two instruments as shown above. The instruments are connected by the Tektronix UltraSync High Performance Synchronization & Control Bus. UltraSync is more that just a common external trigger between two oscilloscopes. External trigger systems often result in acquisition-to-acquisition jitter across multiple channels of several picoseconds which is not precise enough for 100G testing. Instead, UltraSync shares a common 12.5 GHz sample clock across the two instruments. The result is that the two instruments are combined to form a single instrument whose acquisition-to-acquisition jitter across all channels delivers the same level of measurement precision as a standalone, monolithic oscilloscope. And, with this modularity comes flexibility.

In addition to the four 33 GHz channels, the DPS77004SX oscilloscope system offers two 70 GHz channels. By simply switching from the 33 GHz channels to the 70 GHz channels, the oscilloscope bandwidth and sample rate can both be doubled. This permits a "peek" at single-polarization 400G signals with the 100G test system.

When the time comes to perform full 400G testing, the original DPS77004SX system can be completely leveraged and another DPS77004SX system, providing two more channels of 70 GHz acquisition, can be added, creating a system that is capable of full dual-polarization coherent optical acquisition - all tied together via UltraSync.

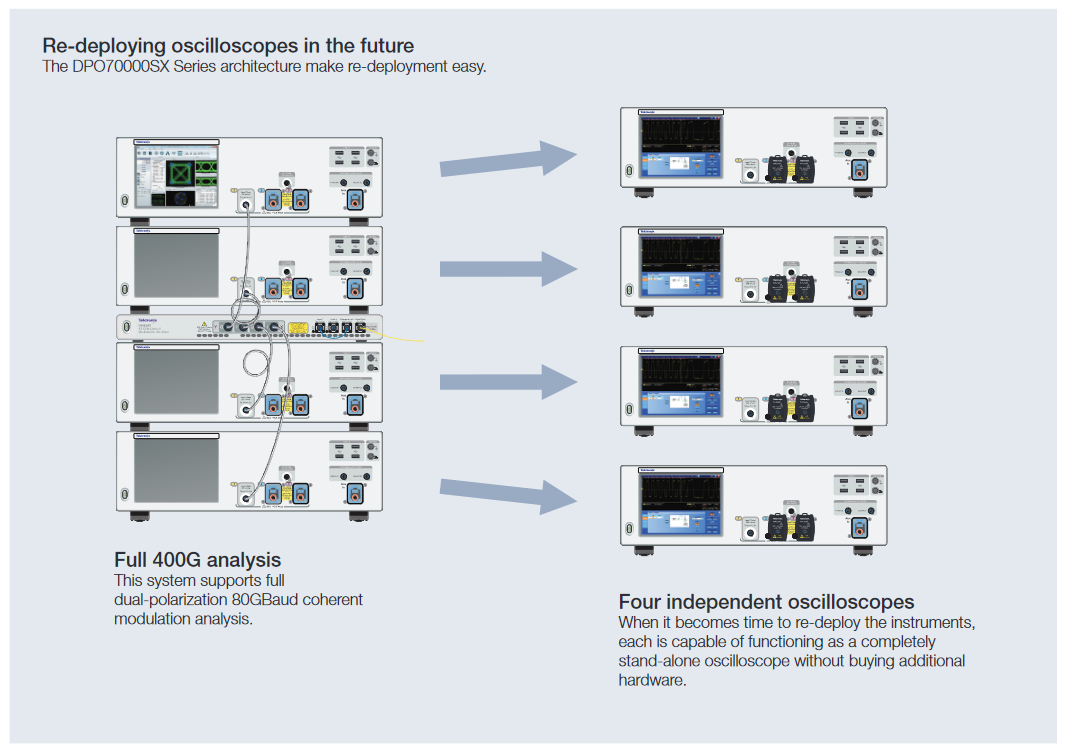
Re-deploying oscilloscopes

As technologies progress and testing requirements evolve, it's common to re-deploy instruments from one lab or development team to another within the company or institution. Here again, the modularity of the DPO70000SX Series oscilloscopes provides a significant benefit.

Systems can easily be scaled down with multiple units divided and redeployed to other projects as needed, maximizing the use of a capital investment. For instance, when a project requiring four 70 GHz channels comes to an end, a lab has the ability to easily redeploy the oscilloscopes to other labs. A fourunit configuration can be divided in half to create two systems or further subdivided into single-unit stand-alone instruments by simply removing UltraSync cables, allowing four projects to each use one instrument.

The DPS77004SX system-based dual-polarization 400G system described above is built up from four individual instruments tied to a common 12.5 GHz sample clock via UltraSync. Each of the four instruments can be operated as a complete stand-alone oscilloscope without any other hardware required. This provides the ultimate flexibility when it comes time to re-deploy the instruments from the original lab to another.

Other multi-instrument oscilloscope architectures employ a master control instrument controlling multiple acquisition instruments. The drawback to this approach is that the acquisition instruments cannot be used on their own. Separating this system into individual oscilloscopes without investing in additional control hardware is simply not possible.

Analysis for Conclusive Evaluation

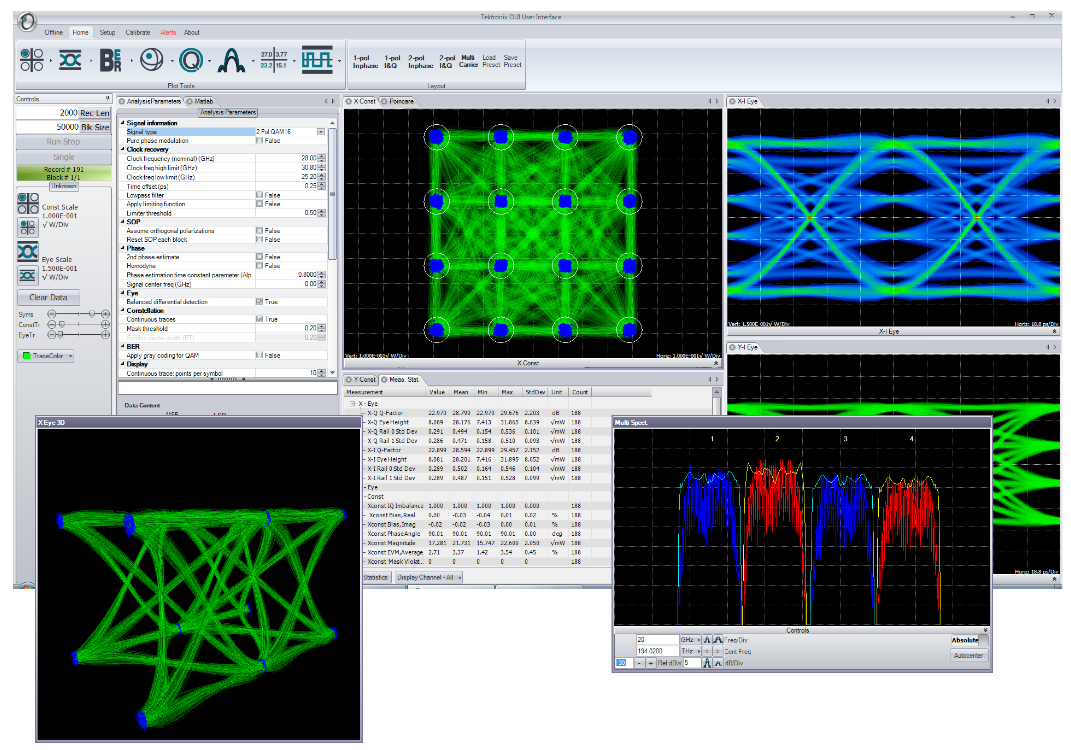
Test and measurement coherent receivers typically come with analysis and visualization software. However, it is not uncommon for designers or researchers to need a particular type of measurement or visualization that is not present in the software from the coherent receiver manufacturer. Or, for example, perhaps the researcher is evaluating the quality of a new phase recovery algorithm. The ideal optical modulation analysis software will provide not only the basic building blocks for measurements, but also allow complete customization of the signal processing.

A common thread throughout the Tektronix OM Series coherent optical products is the OM1106 Coherent Optical Analysis Software. This software is included with all Tektronix OM4000 Series optical modulation analyzers (OMA) and is also available as a stand-alone software package for customers to use with own OMAs or as a coherent optical research tool.

The OM1106 analysis software consists of a number of major building blocks. At the heart of the software is a complete library of analysis algorithms. These algorithms have not been re-purposed from the wireless communications world: instead, they are specifically designed for coherent optical analysis, executed in a customer-supplied MATLAB installation.

The OM1106 software also provides a complete applications programmatic interface (API) to these algorithms. Using these APIs to provide a substantial feature set is the OM Series User Interface (OUI). The OUI provides a complete coherent optical tool suite allowing any user to conduct detailed analysis of complex modulated optical signals without requiring any knowledge of MATLAB, analysis algorithms, or software programming.

The flexibility of the OM1106 software allows it to be used in a number of different ways. You can make measurements solely through the OUI, you can use the programmatic interface to and from MATLAB for customized processing, or you can do both by using the OUI as a visualization and measurement framework around which you build your own custom processing.

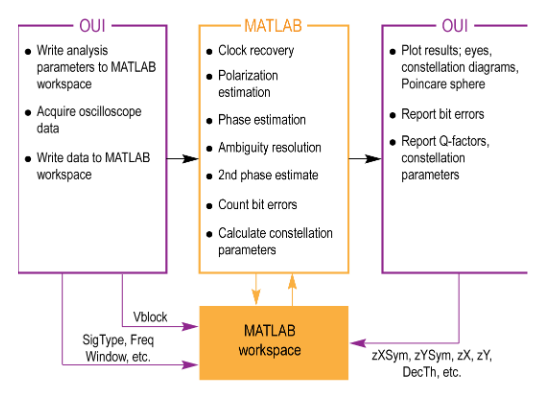
Interaction between OUI and MATLAB

The OUI takes information about the signal provided by the user together with acquisition data from the oscilloscope and passes them to the MATLAB workspace as shown. A series of MATLAB scripts are then called to process the data and produce the resulting field variables. The OUI then retrieves these variables and plots them. Automated tests can be accomplished by connecting to the OUI or by connecting directly to the MATLAB workspace.

The user does not need any familiarity with MATLAB; the OUI can manage all MATLAB interactions. However, advanced users can access the MATLAB interface internal functions to create user-defined demodulators and algorithms, or for custom analysis visualization.

Signal processing approach

For real-time sampled systems, the first step after data acquisition is to recover the clock and retime the data at 1 sample per symbol at the symbol center for the polarization separation and following algorithms (shown as upper path in the figure).

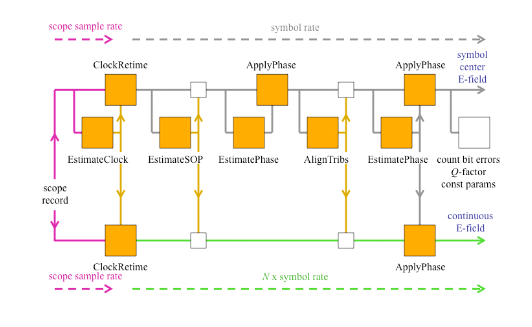
The data is also re-sampled at 10X the baud rate (user settable) to define the traces that interconnect the symbols in the eye diagram or constellation (shown as the lower path).

The clock recovery approach depends on the chosen signal type. Laser phase is then recovered based on the symbolcenter samples. Once the laser phase is recovered, the modulation part of the field is available for alignment to the expected data for each tributary. At this point bit errors can be counted by looking for the difference between the actual and expected data after accounting for all possible ambiguities in data polarity. The software selects the polarity with the lowest BER. Once the actual data is known, a second phase estimate can be done to remove errors that may result from a laser phase jump. Once the field variables are calculated, they are available for retrieval and display by the OUI.

At each step the best algorithms are chosen for the specified data type, requiring no user intervention unless desired.

Signal processing customization

The OM1106 software includes the MATLAB source code for the "CoreProcessing" engine (certain proprietary functions are provided as compiled code). You can customize the signal processing flow, or insert or remove processes as desired. Alternatively, you can remove all Tektronix processing and completely replace it with your own. By using the existing variables defined for the data structures, you can then see the results of analysis processing using the rich visualizations provided by the OUI. This allows you to focus your time on algorithms rather than on tasks such as acquiring data from the oscilloscope or building a software framework to display constellation diagrams.

Dynamic MATLAB integration

Customizing the CoreProcessing algorithms provide an excellent method of conducting signal processing research. In order to speed up development of signal processing the OM Series User Interface (OUI) provides a dynamic Matlab integration window. Any Matlab code typed in this window is executed on every pass through the signal processing loop. This allows you to quickly add or "comment out" function calls, write specific values into data structures, or modify signal processing parameters on the fly without having to stop the processing loop or modify the Matlab source code.

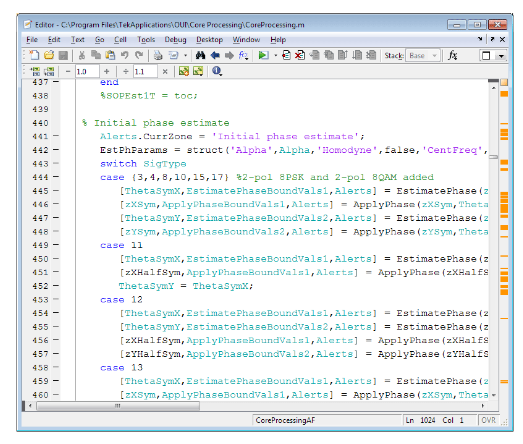
CoreProcessing functions

The following are some of the CoreProcessing functions used to analyze the coherent signal. Full details on these functions, their use in the processing flow, and the MATLAB variable used, are available in the OM1106 user manual.

EstimateClock determines the symbol clock frequency of a digital data-carrying optical signal based on oscilloscope waveform records. The scope sampling rate may be arbitrary (having no integer relationship) compared to the symbol rate.

ClockRetime forms an output parameter representing a dualpolarization signal vs. time, from four oscilloscope waveforms. The output is retimed to be aligned with the timing grid specified by Clock.

EstimateSOP reports the state of polarization (SOP) of the tributaries in the optical signal. The result is provided in the form of an orthogonal (rotation) matrix RotM. For a polarization multiplexed signal the first column of RotM is the SOP of the first tributary, and the second column the SOP of the second tributary. For a single tributary signal, the first column is the SOP of the tributary, and the second column is orthogonal to it. The signal is transformed into its basis set (the tributaries horizontal vertical polarizations) by multiplying by the inverse of RotM.

EstimatePhase estimates the phase of the optical signal. The algorithm used is known to be close to the optimal estimate of the phase. The algorithm first determines the heterodyne frequency offset and then estimates the phase. The phase reported in the .Values field is after the frequency offset has been subtracted.

ApplyPhase multiplies the values representing a single or dual polarization parameters vs. time by a phase factor to give a resulting set of values.

AlignTribs performs ambiguity resolution. The function acts on variable which is already corrected for phase and state of polarization, but for which the tributaries have not been ordered. AlignTribs uses the data content of the tributaries to distinguish between them. AlignTribs processes the data patterns in order according to the modulation format, starting with X-I. For each pattern it tries to match the given data pattern with the available tributaries of the signal. If the same pattern is used for more than one tributary, the relative pattern delays will be used to distinguish between them.

The use of delay as a secondary condition to distinguish between tributaries means that AlignTribs will work with transmission experiments that use a single data pattern generator which is split several ways with different delays. The delaysearch is performed only over a limited range of 1000 bits in the case of PRBS patterns, so this method of distinguishing tributaries will not usually work when using separate data pattern generators programmed with the same PRBS.

Spect estimates the power spectral density of the optical signal using a discrete Fourier transform. It can take any many time waveforms as input such as corrected oscilloscope input data, front-end processed data, polarization separated data, averaged data, and FIR data. It can also apply Hanning or FlatTop window filters and produce the desired resolution bandwidth over a set frequency range.

GenPattern generates a sequence of logical values, 0s and 1s, given an exact data pattern. The exact pattern specifies not only the form of the sequence but also the place it starts and the data polarity. The data pattern specified may be a pseudo-random bit sequence (PRBS) or a specified sequence.

LaserSpectrum estimates the power spectral density of the laser waveform in units of dBc. The function LaserSpectrum takes ThetaSym, the estimated relative laser phase sampled at the symbol rate, as input and defines the frequency centered laser waveform. This waveform is then scaled by a hamming window, and the power spectral density of the waveform is estimated as the discrete Fourier transform of this signal.

QDecTh uses the decision threshold method to estimate the Q-factor of a component of the optical signal. The method is useful because it quickly gives an accurate estimate of Q-factor (the output signal-to-noise ratio) even if there are no bit errors, or if it would take a long time to wait for a sufficient number of bit errors.

Summary

Complex modulation formats used in the latest 100G and 400G communication technologies present new challenges for the designer when it comes to choices of test equipment. Certain performance parameters such as the coherent receiver bandwidth or oscilloscope sample rate have an obvious impact on the measured signal quality. However, there are a number of other aspects to the choice of a coherent optical acquisition system that may be less obvious but can play an equally key role in a successful test system.

This technical brief examined three such aspects in further detail and showed how they play a vital role in a coherent optical test system:

1. Optimal Error Vector Magnitude (EVM) floor and oscilloscope digitizer effectiveness;
2. Future-proofing the system for next generation communications technology;
3. Analysis techniques for conclusive evaluation.

Visit www.tek.com/coherent-optical-solutions to see how Tektronix can help solve your 100G, 400G and next generation coherent optical designs.