Introduction
Noise, or more specifically the voltage and current fluctuations caused by the random motion of charged particles, exists in all electronic systems. An understanding of noise and how it propagates through a system is a particular concern in RF and microwave receivers that must extract information from extremely small signals. Noise added by circuit elements can conceal or obscure low-level signals, adding impairments to voice or video reception, uncertainty to bit detection in digital systems and cause radar errors. Measuring the noise contributions of circuit elements, in the form of noise factor or noise figure is an important task for RF and microwave engineers. This paper, along with its associated appendices presents an overview of noise measurement methods, with detailed emphasis on the Y-factor method and its associated measurement uncertainties.
Noise Measurements
The noise contribution from circuit elements is usually defined in terms of noise figure, noise factor or noise temperature. These are terms that quantify the amount of noise that a circuit element adds to a signal. They can be measured directly using available test equipment as well as modeled using both system and circuit simulation SW.
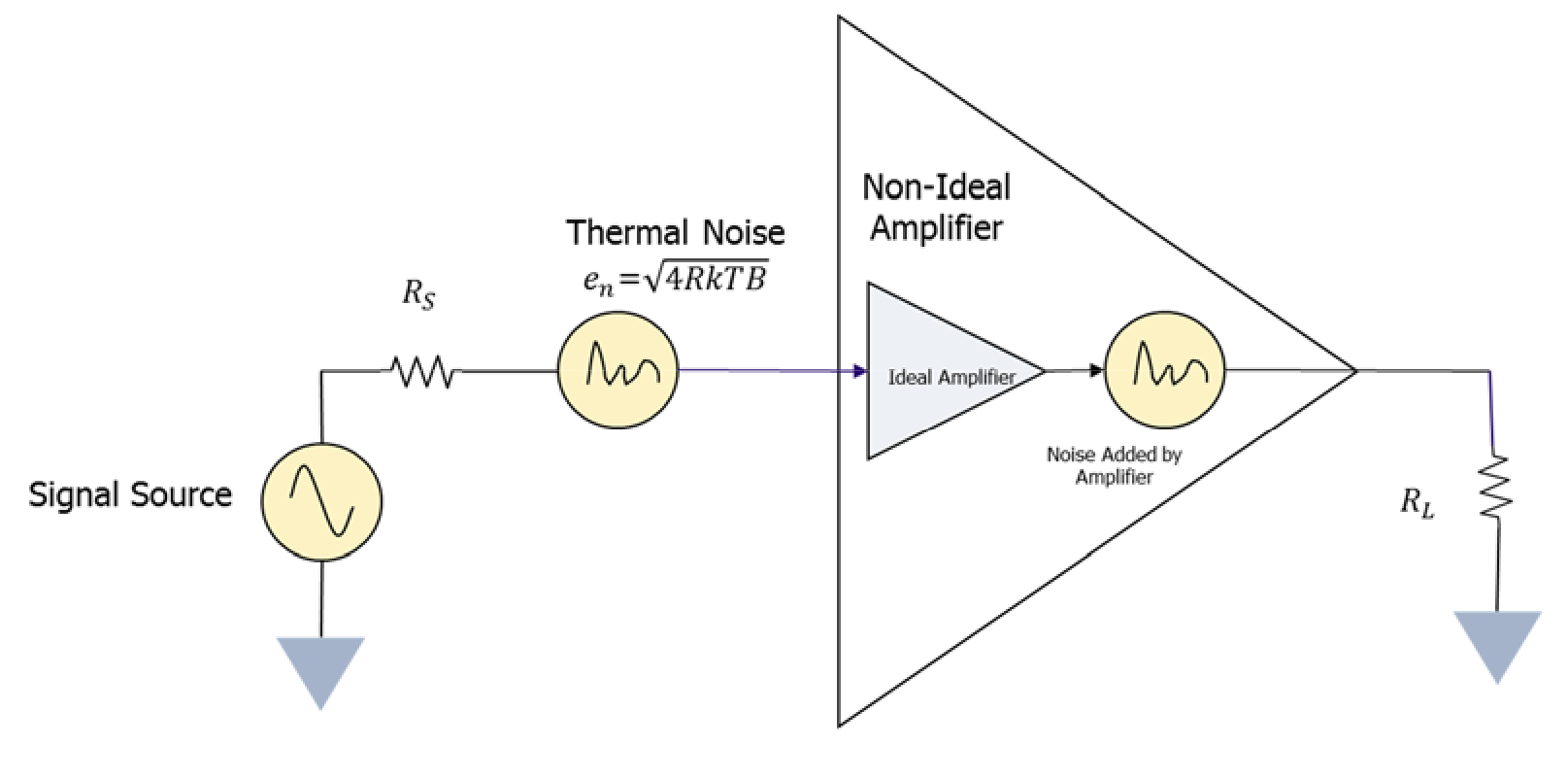
Consider the amplifier1 shown schematically in Figure 1. Its intended job is to amplify the signal presented at its input and deliver it to the load. The thermal noise that is present at the input is amplified along with the input signal. The amplifier also contributes additional noise. The load receives a composite signal made up of the sum of the amplified input signal, the amplified thermal noise and the additional noise contributed by the amplifier. Noise figure, noise factor and noise temperature are figures of merit used to quantify the noise added by a circuit element, the amplifier in this case.
Noise Factor, Noise Figure and Noise Temperature
Noise factor is defined as the signal-to-noise ratio at the input divided by the signalto-noise ratio at the output. Noise factor is always greater than unity as long as the measurement bandwidth is the same for the input and output.

Noise figure is Noise Factor expressed in dB.
The definitions for noise figure and noise factor are valid for any electrical network, including frequency converting networks that contain mixers and IF amplifiers (up-converters or downconverters).

Active Devices
If we consider an electrical network such as amplifier or frequency converter with input signal S(ω), voltage gain A(ω) and additive noise referred to the output of NA(ω) we have

where Nin is the noise present at the input to the system. The parenthetical (ω) is used to indicate that these are frequency-dependent quantities. For simplicity, we will drop this functional notation in the remainder of the paper unless it is needed for clarity.

An important case exists when the noise at the input is thermal noise, NT. NT has a flat power spectral density with power level of |NT(ω)|2 = kTB. k refers to Boltzmann’s constant, T ܶto the absolute temperature in degrees Kelvin and B to the system bandwidth expressed in Hertz. kTB ݇at 300 Kelvin has a value of 4.14X10-21 W or -174 dBm when measured in a one Hz bandwidth.
Similarly, the signal-to noise ratio at the output is given by

where A is the voltage gain of the device under test (DUT) and NA is the noise voltage added by the DUT. The noise factor can be computed by taking the ratio.

It is often more practical to use power gain instead of voltage gain. Let the power gain of the system be
G = |A|2
Equation 5 becomes

In the case where the input noise is thermal noise or KT0B

T0 in the above equation refers to a standard temperature, usually 290K.
Noise factor and noise figure are an indication of the excess noise (beyond the system thermal noise) contributed by a functional block in a system.
Effective noise temperature refers to the temperature that a matched input resistance would require to exhibit the same added noise.

Effective noise temperature can be related to noise factor by
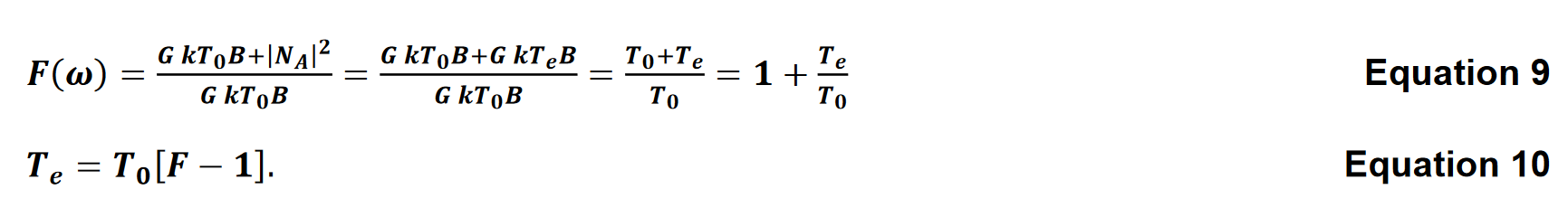
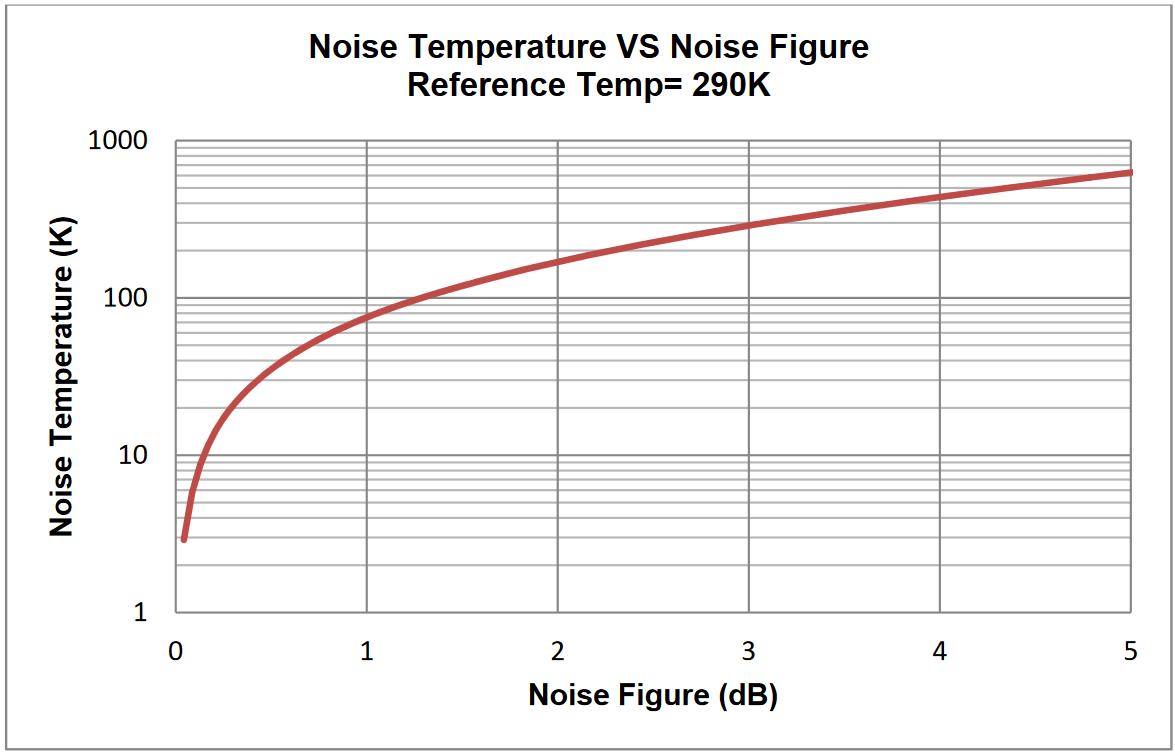
T0 is the reference temperature, usually 290K. Figure 2. Noise Temperature vs. Noise Figure shows a graph of Noise Temperature versus Noise Figure. A noiseless device has a noise temperature of absolute zero or 0 K, while a 4 dB noise figure is equivalent to a noise temperature of approximately 430 K.
Passive Devices
Passive devices, those composed only of resistive or reactive elements, have a power gain less than or equal to unity and contribute no additive noise beyond thermal noise. The noise power at the output when the input is terminated is always kTB .Applying Equation 5 and Equation 6 we have

The above equation states that the noise figure of a passive device is the reciprocal of its power gain. A 3 dB attenuator ( G = 1/2 ) for example would have a 3 dB noise figure.
Noise Figure of Cascaded Stages
Consider a two-port network consisting of two stages. The first stage has thermal noise present at its input. This thermal noise is amplified by the first stage gain and has any additive noise produced by the first stage added to it. The noise at the output of the first stage is then

The second stage has the output of the first stage presented to it. The second stage amplifies the input and contributes additional noise.
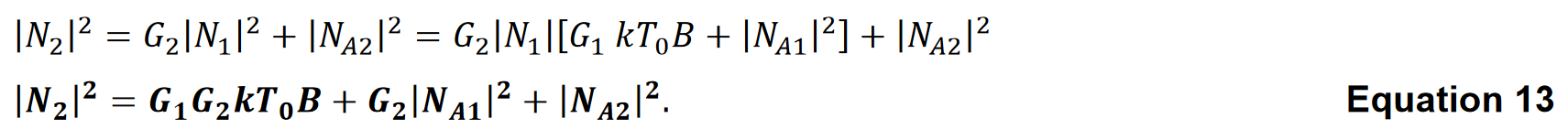
The principle illustrated above can be extended for multiple stages.
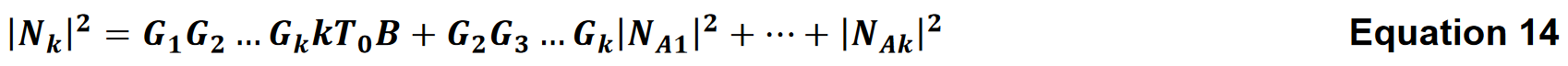
The noise factor is the ratio of the SNR at the input to the SNR at the output. For a given input signal, the ratio for a cascade of k stages is
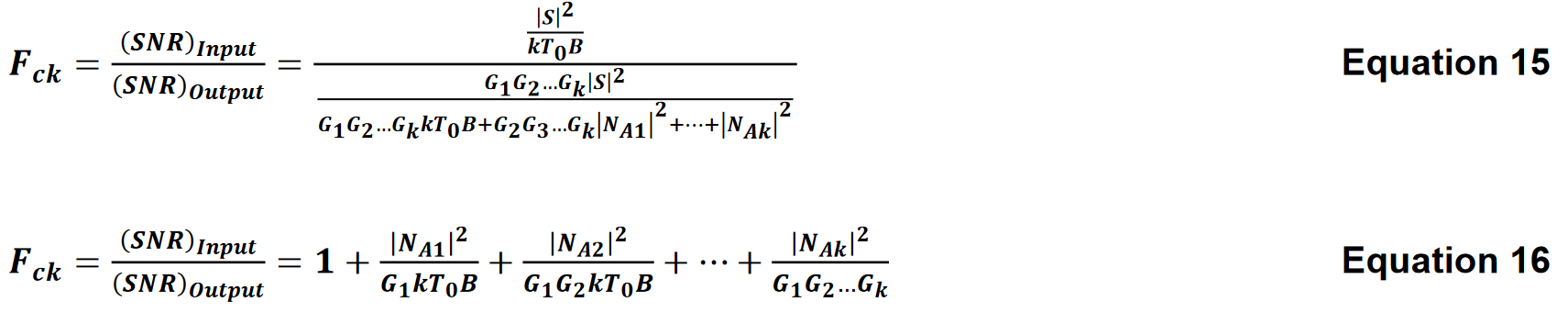
Applying Equation 6 to Equation 16 yields the noise figure calculation for a system consisting of k cascaded stages. Consider K stages in a system. The kth stage has power gain GK and noise factor Fk Both the signal and the noise from previous stages arrive at the input of the kth stage. The contribution of the kth stage is reduced by the gain preceding it. Noise Figure calculation for the cascade of K stages can be found from
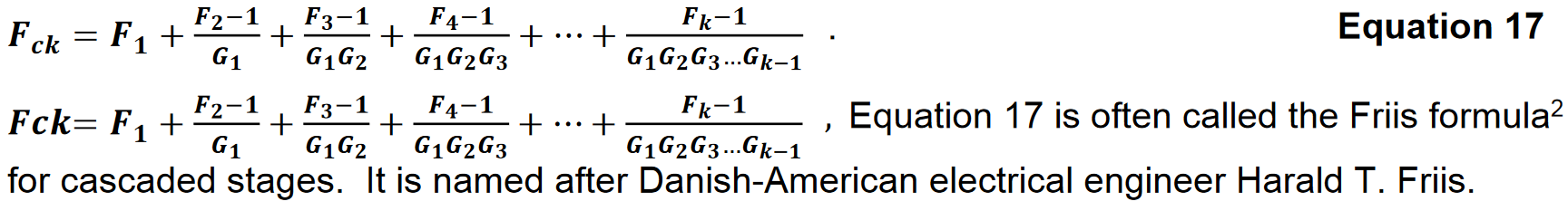
Effective Noise Temperature of Cascaded Stages
The same equation can be manipulated to give the effective noise temperature for cascaded stages. If we replace the noise factors of each stage by their effective noise temperature we get
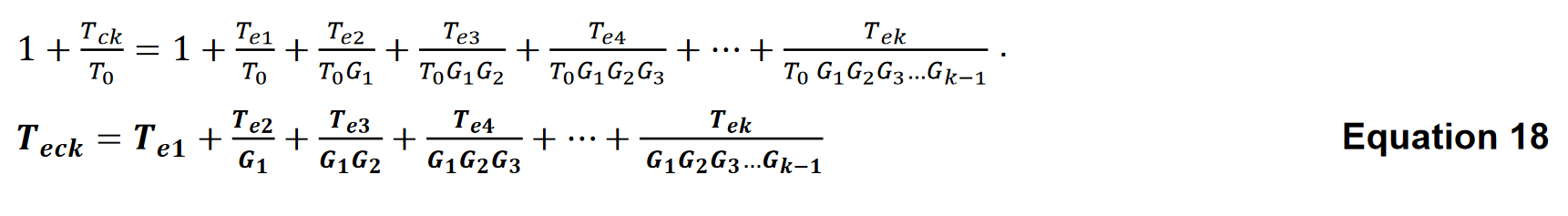
Noise Figure Measurements
Y-factor Method
The Y-factor method uses a noise source that can be switched off and on. It is based on two power measurements, each performed with the same port impedances3 and the same measurement bandwidth. The Noise source has a specified amount of excess noise. This is specified as the Excess Noise Ratio or ENR. ENR is the ratio of noise from the source to the system thermal noise or kTB, often expressed in dB.
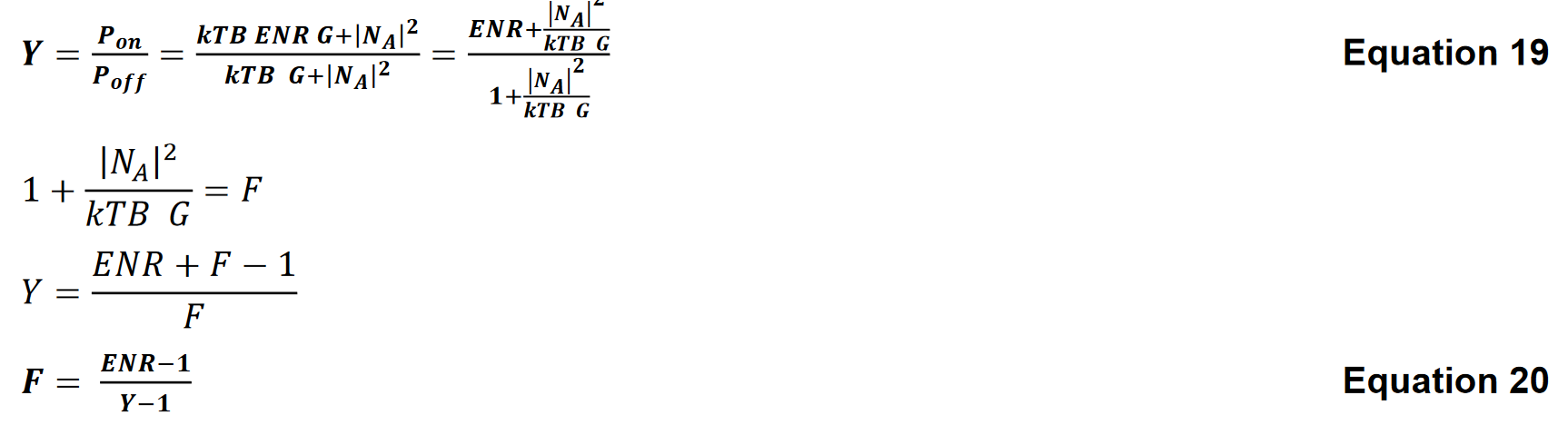
Making a noise figure measurement using the Y-factor method involves the use of a switchable noise source and four power measurements. The first two measurements are used to characterize the noise behavior of the receiver used to make measurements. P1 ,is the power measured by the measuring receiver with the noise source in the OFF state. P2, is the power measured by the measuring receiver with the noise source in the ON state. The device under test (DUT) is inserted between the noise source and the receiver for the next two power measurements. P3 and P4 are the power measurements made at the DUT output with the noise source turned OFF and ON respectively.
There are then three steps in making the measurement. The first, often called the calibration step, is to measure the noise figure of the RF receiver used to make the power measurements. The second step is to make a noise figure measurement on the cascaded receiver and DUT. The next step is to de-embed the two measurements.
Let the receiver noise figure be

The noise figure for the cascade of DUT and receiver has a

The power gain of the DUT is measured by taking the ratio
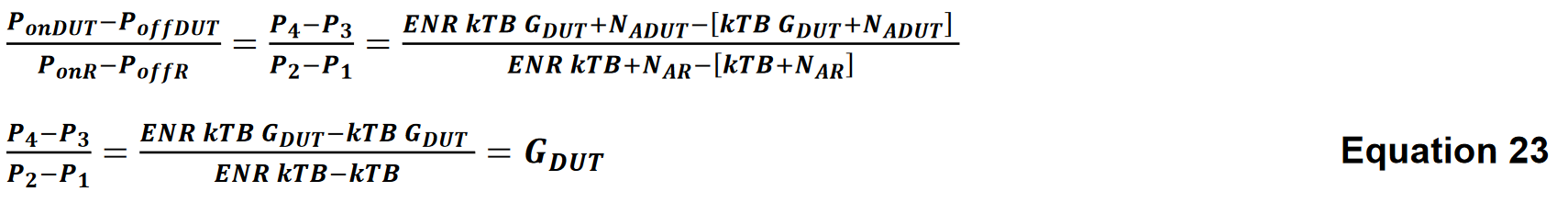
From the cascaded noise figure equation we have
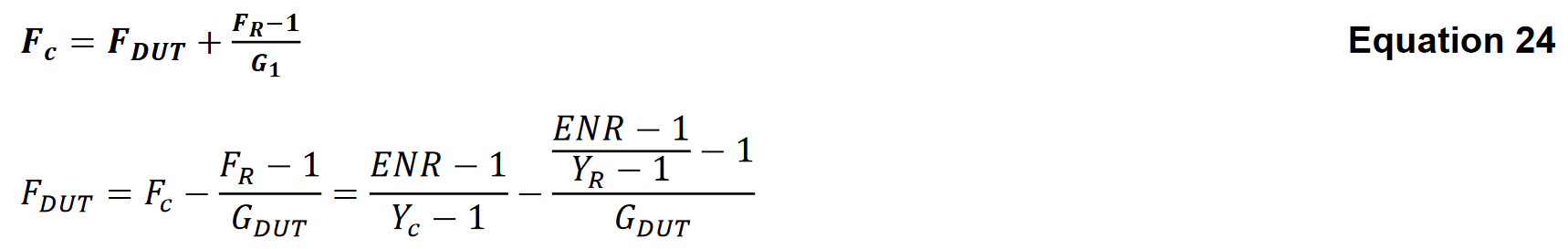
Substituting the power ratios for the Y-factors, we get
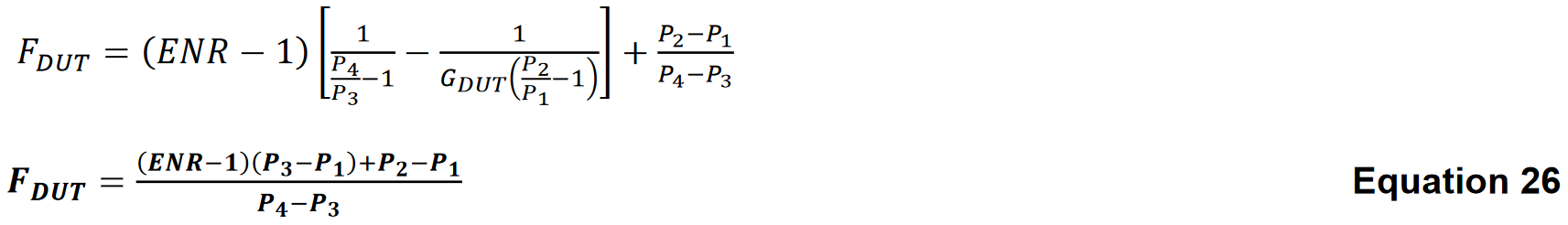
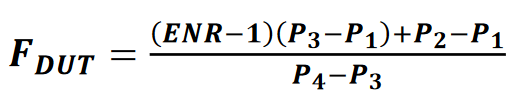
Equation 26 expresses the noise figure of the device under test in terms of the four power measurements in the Y-factor method. This method relying on a series of power measurements is ideally suited to low-level measurement receivers. It has been implemented in modern spectrum analyzers as a cost-effective method of making noise figure measurements.
Cold Source or Network Analyzer Method
The cold source method essentially measures the noise power at the output of a device with an input that is at the reference temperature (cold). It depends on very accurate knowledge of the device gain. Network Analyzers can measure gain with extreme accuracy, making them ideal for this method. Like the Y-factor Method, the cold source method requires a calibration step to determine the measurement receiver’s noise figure. This is done with the use of a calibrated noise source and a method similar to what is described in Equation 21.
The gain of the device under test is then measured as a function of frequency using the usual network analyzer methodology. A power measurement is then made as function of frequency with the cold source connected to the device under test. If we let ܰܰNA(ω) be the noise added by the device under test and ܰNR(ω) be the noise added by the receiver then the measured power is
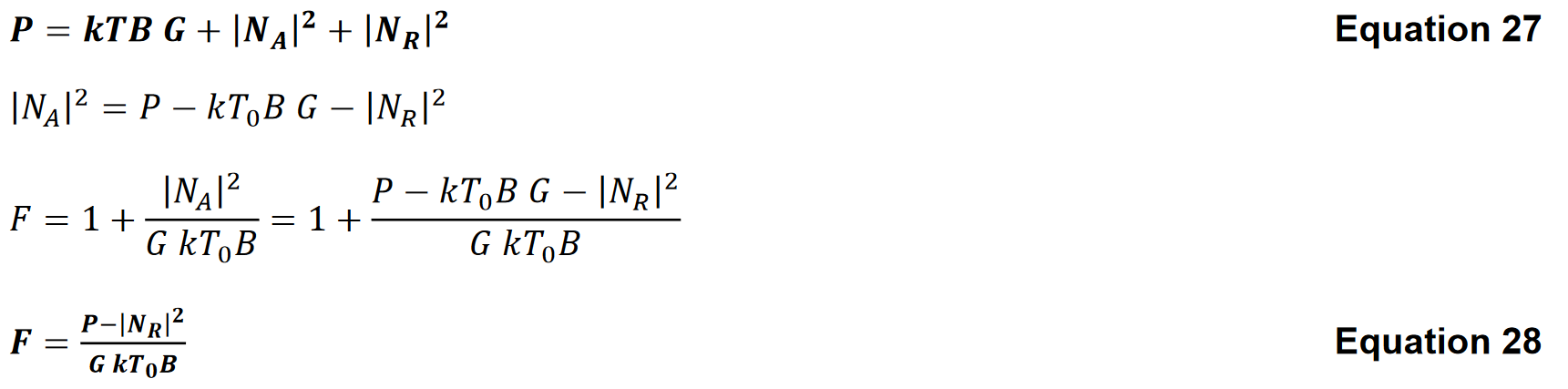
Some network analyzers4 offer a noise figure measurement option that includes low noise preamplifiers in their receivers, calibrated noise sources and the software to make measurements. The Network Analyzer’s ability to make accurate transmission and reflection measurements means that complete characterization of devices can be made that include Noise Figure and S-parameters, making Network Analyzer measurements ideal for inclusion in software-based system models.
Signal Generator (Twice Power) Method
Measuring devices with a high noise figure presents a problem for the popular Y-factor method. The Y-factor approaches unity as the noise figure approaches the source ENR. This affects the accuracy of the Y-factor measurement. The twice-power method uses a signal generator and a measuring receiver with an accurately known noise BW such as a spectrum analyzer. The input to the device under test is terminated with a load at approximately the reference temperature (usually 290K). A signal generator is then connected to the device under test until the measured power is exactly 3 dB or twice the power measured with the input terminated. At this point the sinusoidal power is exactly the same as the noise power and the noise factor can be calculated. Knowledge of receiver bandwidth is critical but of knowledge of device gain is not needed. The noise factor of the cascaded DUT and receiver can be computed from

The noise factor for the DUT can be dis-embedded using the formula for cascaded noise figure in Equation 24.
Direct Noise Measurement Method
Devices with high noise figure can be measured with directly with a spectrum analyzer or other receivers with accurately known bandwidths as long as the gain is known. The input to device under test is terminated in a source that is near the reference temperature (290K). The noise power at its output is measured and noise factor can be computed from

Knowledge of receiver bandwidth is required, as is knowledge of device gain. The noise factor of the cascaded DUT and receiver can be computed from the formula for cascaded noise figure in Equation 24.
Noise Figure Measurements in Frequency Converters
The super-heterodyne receiver is at the core of most RF communications systems in use today. The super-heterodyne receiver’s ability to provide high gain and frequency selectivity by performing key filtering and amplification functions at a fixed intermediate frequency (IF) makes it the architecture of choice for sensitive receivers ranging from AM radios to the receivers tracking deep space probes.
The core of the super-heterodyne radio receiver is a frequency conversion (mixing), sometimes done in several stages that transfers the information contained spectrum surrounding the carrier to an IF. The noise performance of frequency converters is therefore a key aspect of receiver design.
Measuring the noise figure, noise factor or noise temperature of receivers and frequency converters is similar to the methodology described above for elements that operate at a single frequency, with the exception that the band of frequencies at the input is not the same as the band of frequencies at the output. Care must also be taken to account for the dual sideband nature of mixers and the multiple conversions in samplers and other harmonic mixing devices.
Frequency Converters with Image Rejection
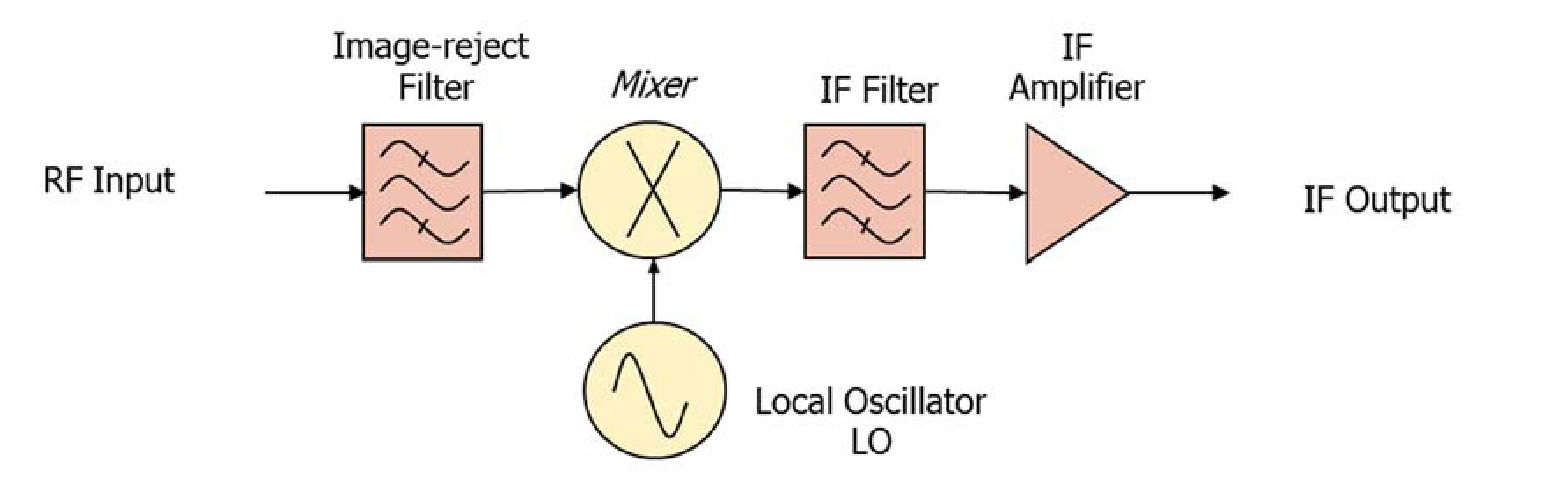
Typical frequency converters used in RF receivers incorporate an image-reject filter prior to the mixer. The image-reject filter is necessary because of the dual sideband nature of sinusoidal multiplication.
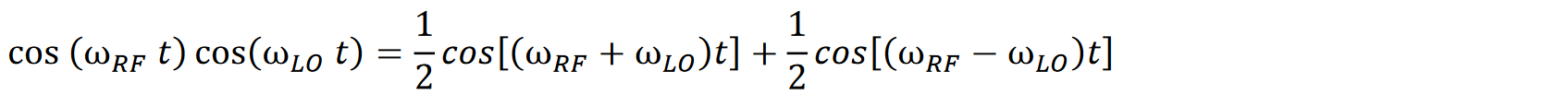
The sum terms above are rejected by the IF band-pass filter, leaving two possibilities for signals to appear within the IF filter.

The above equation has two possible solutions.

The image-reject filter is designed to pass only the upper or only the lower sideband, but not both as shown in Figure 4.
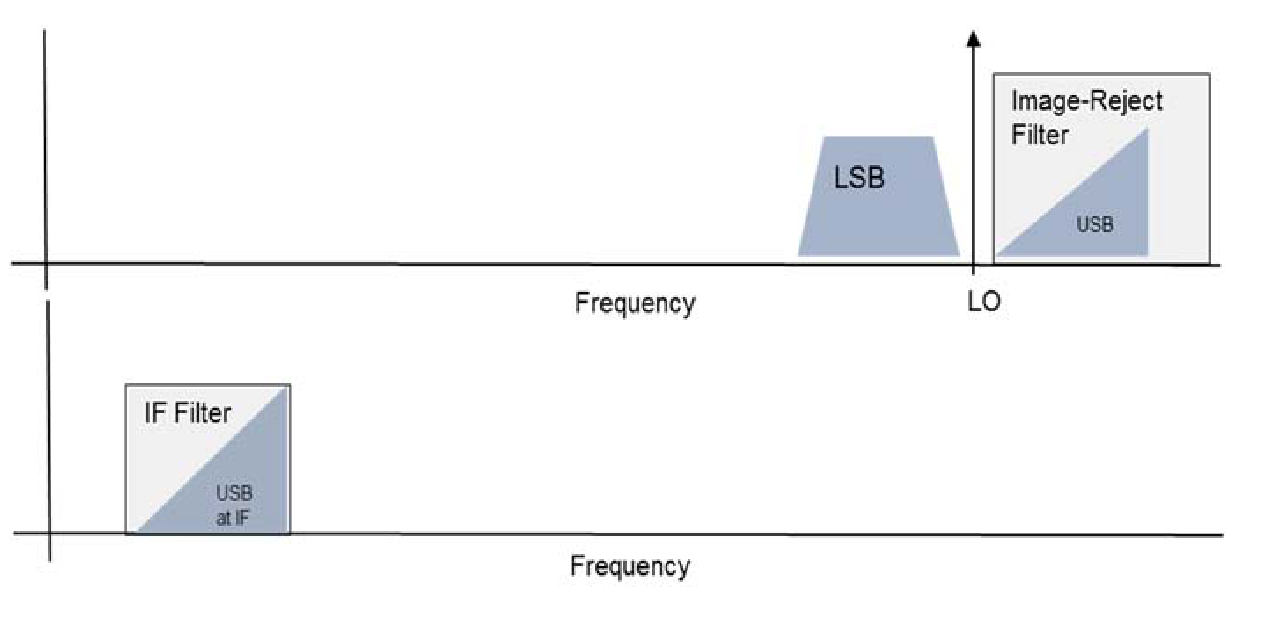
Noise can be represented as a broadband random process with frequency content across all frequencies. Thermal noise is generated in all resistive devices. Shot noise is generated because of the granular nature of electric currents where discrete electrons flow. There are noise generators at every stage in the system shown in Figure 3. Noise components generated prior to the image-reject that lie outside the filter pass-band will be removed by the filter. Both sidebands of noise components generated after the filter will be converted by the mixer. Passive filters are mostly reactive and therefore exhibit no thermal noise. One can then assume that all noise added by the circuit elements in a mixing stage comes from elements located after filtering. Noise from both sidebands is therefore present in the IF, even though the signal from the rejected sideband is not.
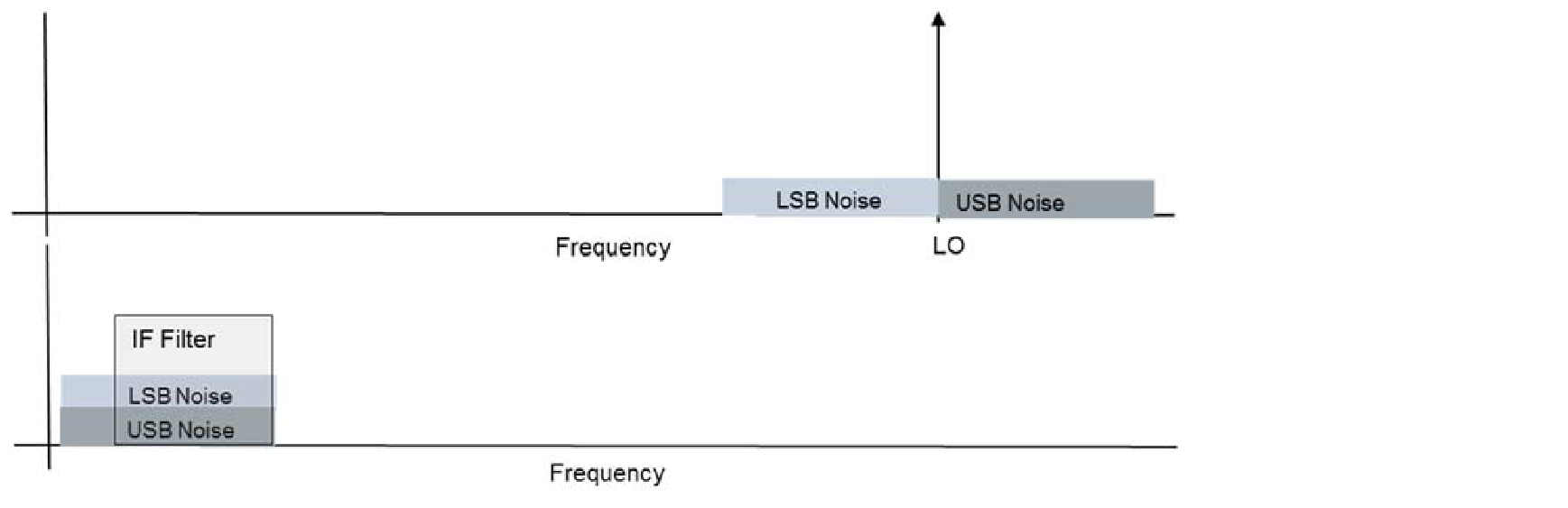
The additional noise from the rejected sideband is indistinguishable from any noise that is added by the system and is generally included in the noise figure measurement of receivers. There are, however, some cases that require special attention.
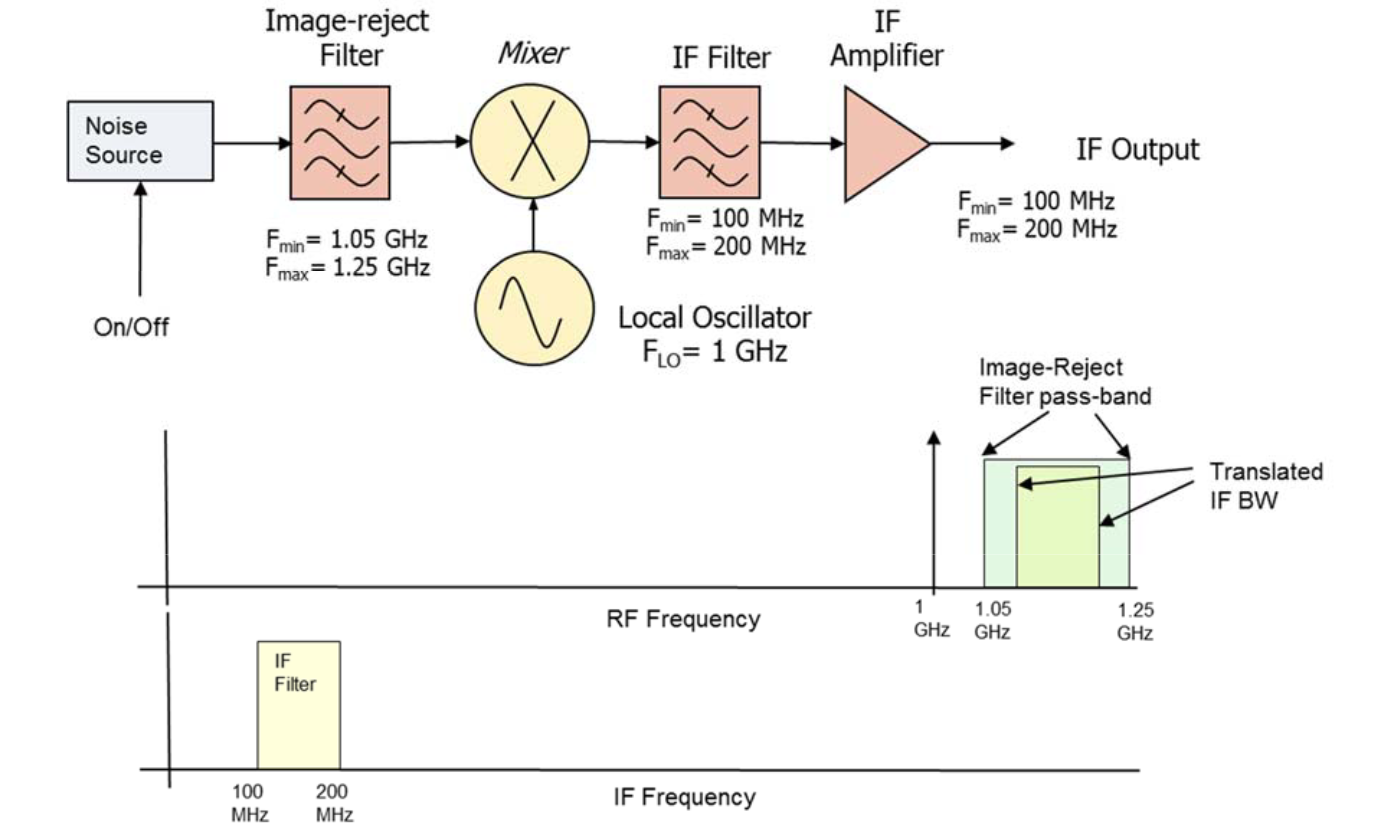
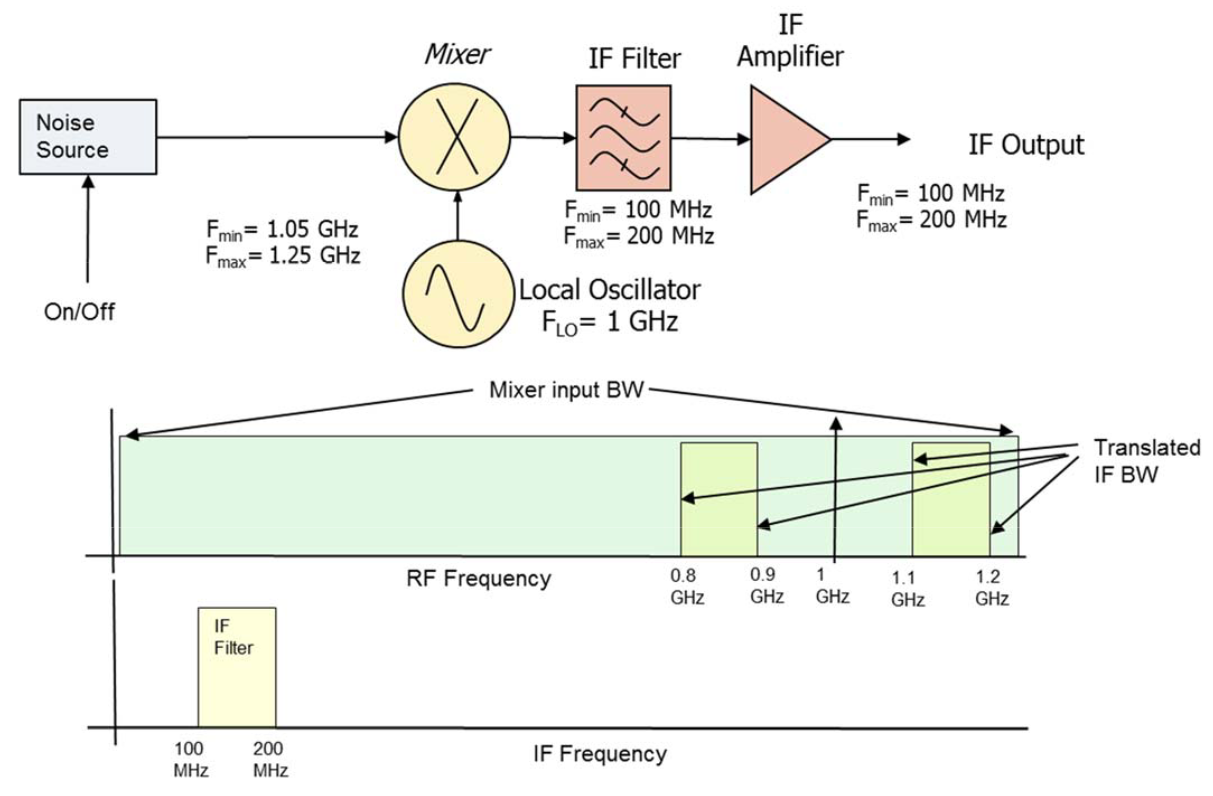
Consider a noise figure measurement made in a frequency converter system as shown in Figure 6. The image-reject filter ahead of the mixer allows the only the excess noise from the noise source that falls in the desired sideband (1.05 GHz to 1.25 GHz) to enter the mixer, while thermal noise from both sidebands enters the mixer. Measurements in such a system are straightforward with the exception that the effect of the frequency converter must be considered.
The noise figure measurement is done in two parts as detailed in Equation 20 – Equation 23. The first part measures the Y-factor of the measuring receiver. This is done at the frequency band that exists after the mixer and IF filter. The frequency converter provides a frequency translation so that the Y-factor measurement for the combined DUT and measuring receiver is done at the band of frequencies that exists before the mixer. A spectrum analyzer performing the noise power measurements needs to be tuned so that it covers the 100 MHz to 200 MHz If in its span. The X-axis of a noise-figure VS frequency plot needs to show the equivalent RF frequency, covering 1.1 GHz to 1.2 GHz.
The noise figure measurement for a frequency converter can be examined by modifying Equation 20 – Equation 24 to include the different bands. If we denote frequencies belonging to the band that precedes the mixer as ω1, and frequencies from the band that exists after the mixer as ω2, then the noise factor of the receiver, done at the after-mixer band is

The noise figure for the cascade of DUT and receiver is measured at the mixer-input band is

The conversion gain of the DUT expressed as a power ratio is measured by taking the ratio

The subscript 1-2 in Equation 27 is used to denote that the gain in question is the frequency conversion gain or the ratio of the power at ω1 to the power at ω2.
From the cascaded noise figure equation we have
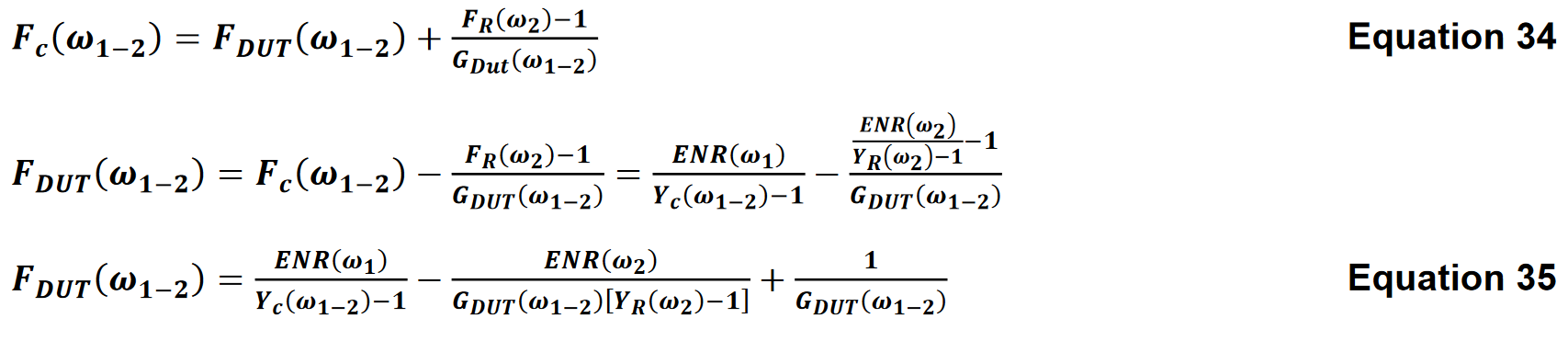
It is important to note that there are two different values of ENR used in Equation 35. The ENR of the noise source at the IF (mixer output frequency) is used when measuring the receiver alone. The ENR of the noise source at the mixer input frequency is used when the frequency converter is in the measurement.
Image-reject Filter is Excluded in the Measurement
Modular systems often place image-reject filters in separate modules from mixers and IF filters. It is often useful to make noise figure measurements in a frequency converter that is separated from its intended image-reject filter. Measurements in such a system will include noise components from both the upper and lower sidebands as shown in Figure 7. The measurements must be adjusted to account for the differences in the operating environment, which includes the image-reject filter, and the test environment which does not.
Figure 7shows an example of a measurement where the image-reject filter is not included. The noise source contributes noise at both the upper and lower sidebands, both of which are converted to the same band at IF.
The Y-factor measurement equation for measuring the receiver is unchanged from Equation 18. The Y-factor measurement equation for the double sideband converter must be modified to account for the contribution from both sidebands. If ENRUω1 and ENRLω1 are the excess noise ratio at the upper sideband and lower sideband respectively, GUω1-2 and GLω1-2 are the upper and lower sideband conversion gains (or losses) expressed as power ratios and |NA(ω2)2| is noise added by the frequency converter stage referred to the post-mixer frequency, then
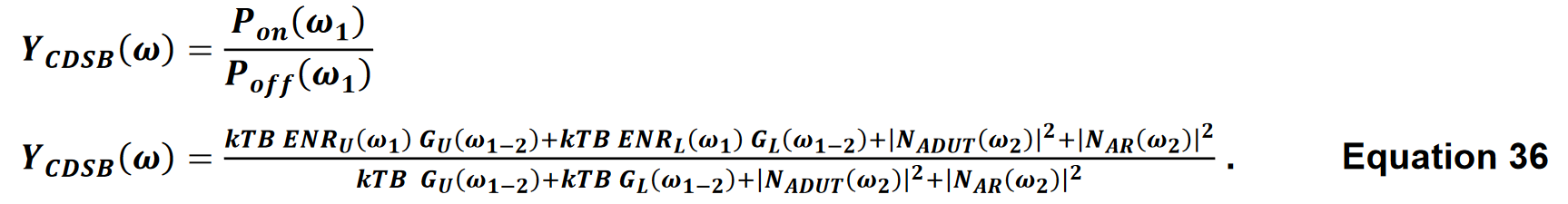
A double-sideband conversion gain for the frequency converter can be measured by taking the ratio
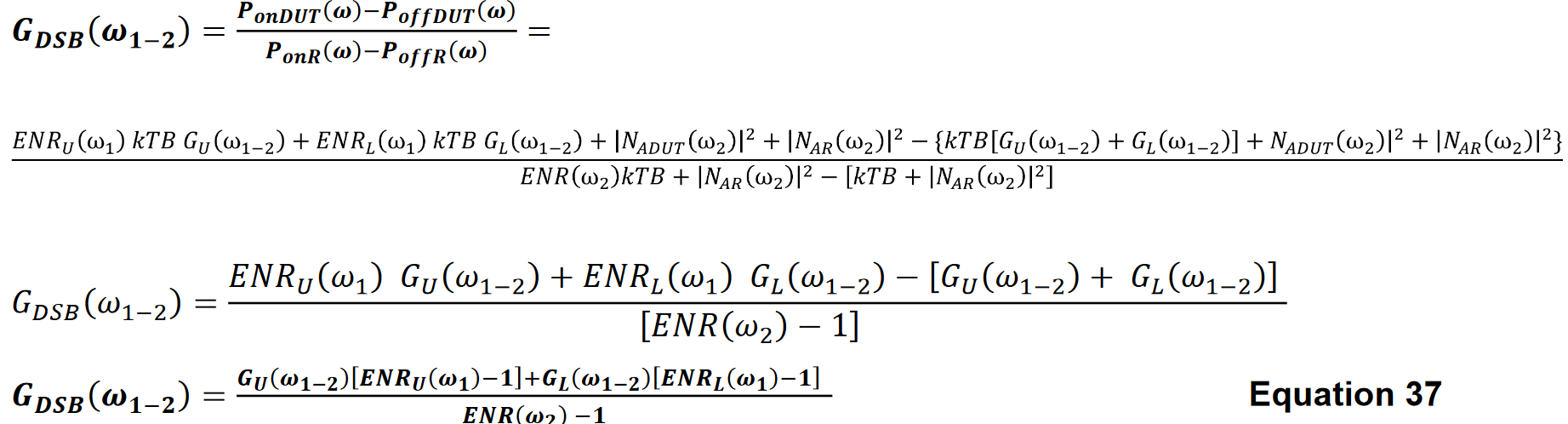
A useful special case of Equation 37 is when the noise source ENR and mixer conversion gain are both constant with frequency.

Equation 37 then simplifies to

In this case, the double-sideband gain is twice the gain of the single sideband case.
The Y-factor for the receiver is measured at the band of frequencies that exists after the mixer.

The Y-factor of the cascaded frequency converter and receiver can be measured. An analysis of this measurement needs to include both the upper and lower sidebands. Let the subscript U denote the upper sideband ENR and gain and the subscript L denote the lower sideband.
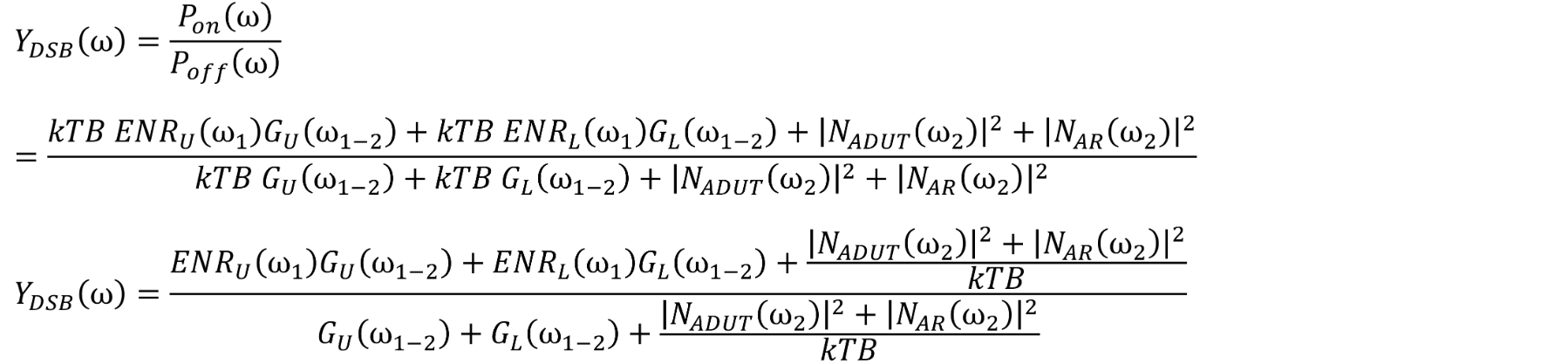
From Equation 31,
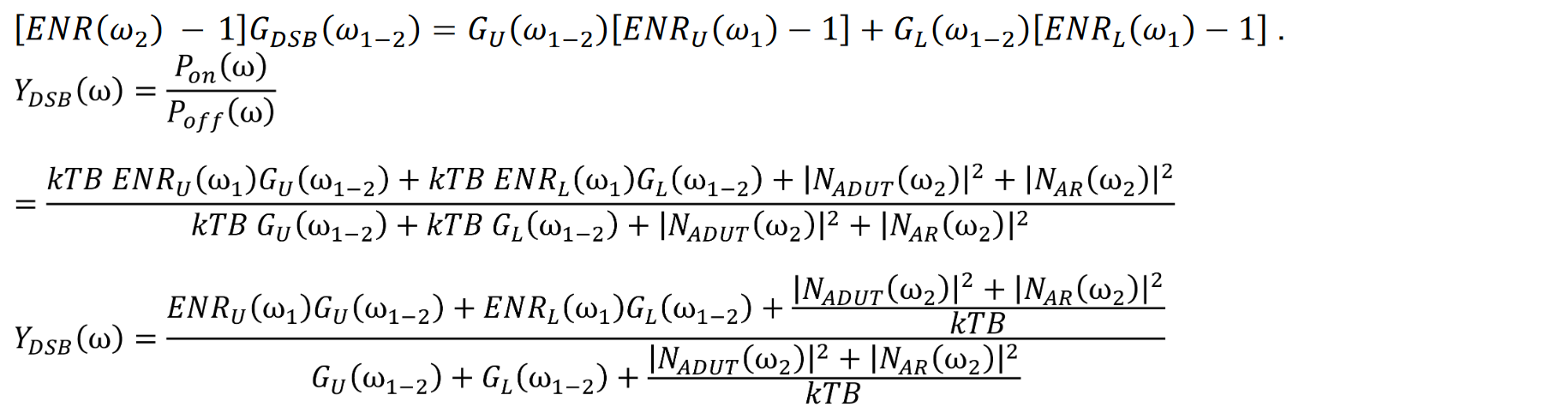
In general, noise figure can be computed using Equation 19, repeated here for convenience.

We must consider three possible values for ENR when measuring a double-sideband mixer. ENRሺωଵሻ and ENRሺωଵሻ refer to the excess noise ratio at the lower and upper sidebands at the mixer inputs. ENRሺωଶሻ refers to the excess noise ratio at the band that exists after mixing. Let us define ENRୈୗ ሺωଵሻ as an effective double-sideband ENR.

Let
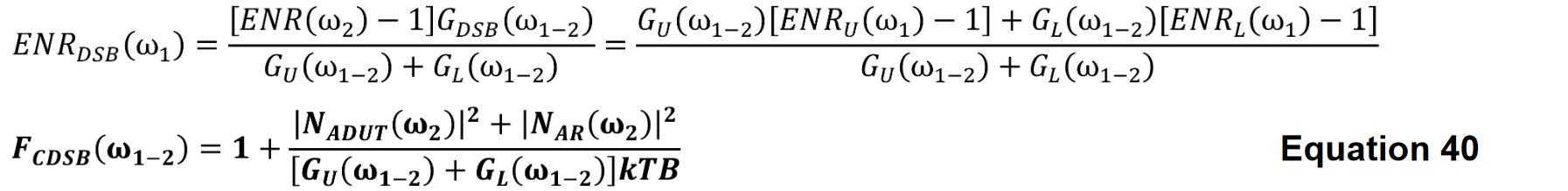
From the equation for cascaded noise factor
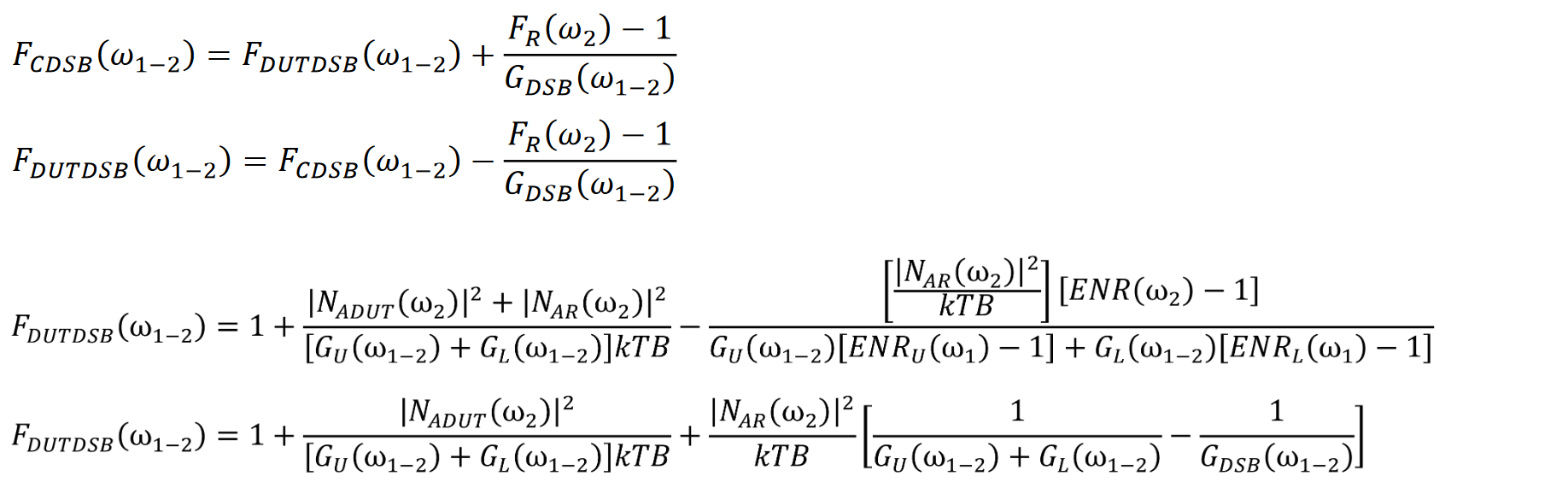
For the case where the conversion gains is flat across the upper and lower sidebands

It should be noted that the noise factor for the case where the image-reject filter is included in the measurement is

One can extend Equation 42 to the lower sideband. For the case where the upper and lower sideband conversion gains are equal and the ENR is flat.
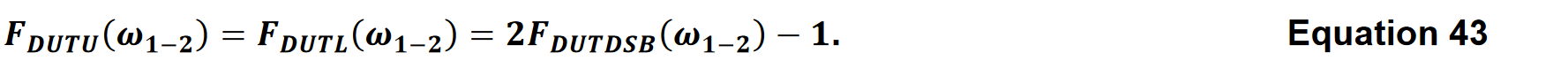
The Nature of Random Noise
Thermal Noise
Everything in the universe is in motion. Even objects that are apparently still have random vibrations of their molecules. This random vibration is felt by the human senses as heat. Temperature is, in fact, a measure of the average kinetic energy of these random vibrations. The same can be said about the molecules in insulators, conductors and semiconductors, charge carriers (electrons and holes) and all physical structures from which electronic devices are built. The power from thermal noise is given by

The brackets indicate that this is a statistical quantity expressed as an average. The variables in Pn = kTB .Equation 44 are:
Pn = Noise power expressed in watts,
T = Absolute temperature in Kelvin,
B = Bandwidth in Hertz, and
݇k = 1.3806488 x 10-23 Joules / Degree k = Boltzmann’s constant.The thermal noise emanating from electronic components manifests itself as fluctuations in voltage and in current. The statistical distributions of voltage and current are nearly Gaussian when observed within a limited bandwidth.
Power Spectral Density of Thermal Noise
Thermal noise in an ideal resistor is approximately white of most of the frequencies used by RF and microwave engineers. A deviation from this flat frequency distribution exists at very high frequencies, when the quantum nature of electromagnetic waves becomes dominant. The noise power can be obtained from5

Equation 45 includes the photon energy, hf , where h is Planck’s constant. In the great majority of cases, the operating frequencies used by RF and microwave engineers are such that hf / kT ≪ 1 and Equation 46 simplifies to the familiar equation showing a flat power spectral density for thermal noise, Pn(f) = kTB .The exceptions occur at very low noise temperatures and very high frequencies.
Figure 8 shows the quantum effects that color the power spectral density of noise. Thermal noise can be considered to have a flat power spectral density out to 100 GHz or more before the quantum effects become dominant.
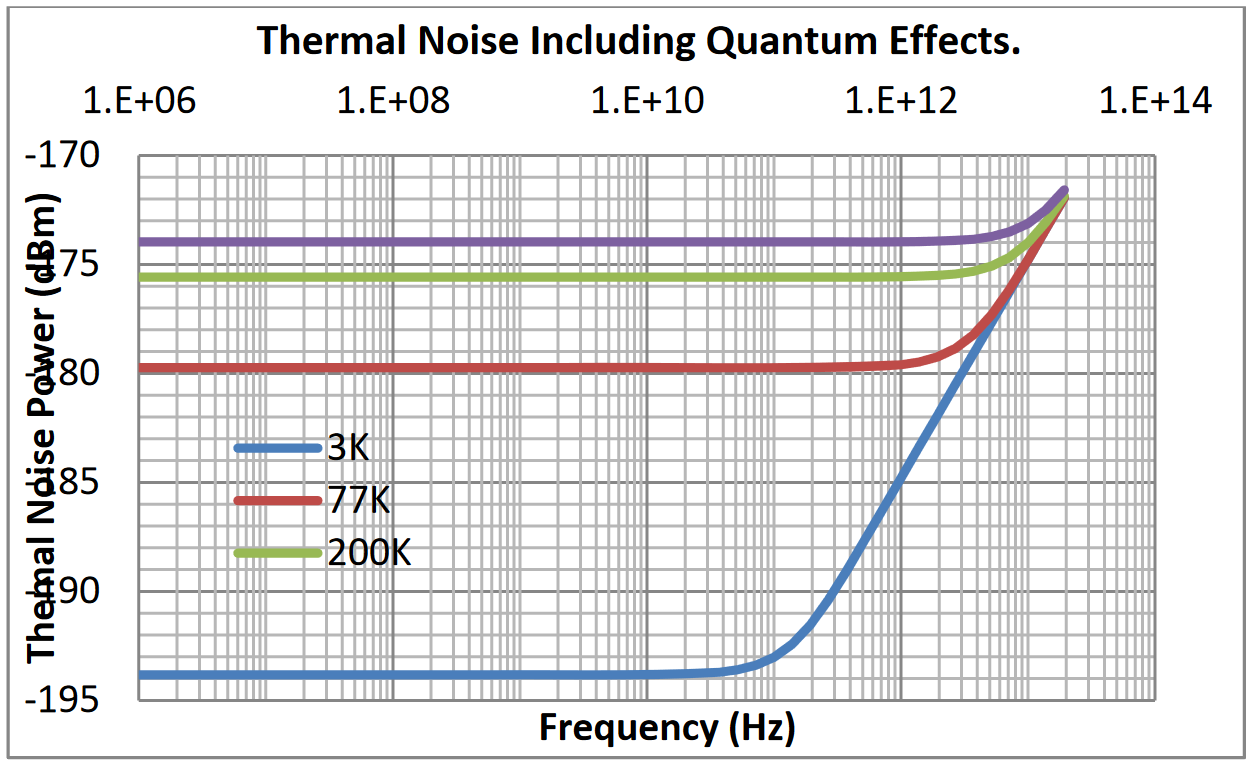
Shot Noise
Engineers usually consider electrical current to be a continuous quantity. In reality it is composed of discrete electrons, each with a fixed charge. Current is quantized. Rather than a continuous flow, current is composed of the effects of individual electrons travelling from the source to the load in a circuit. The electrons arrive with a uniform distribution over time. The effect of this variation in time of arrival is called shot noise or corpuscular noise. Appendix 2 derives the equation for the power spectral density of shot noise. The noise power is proportional to current. The effective noise current approximates a Gaussian distribution with an RMS value or standard deviation given by

i/f Noise
Random fluctuations with a power spectra density that varies approximately as i/f have been observed in many processes ranging from the flooding patterns of the Nile River to the firing of human brain neurons. Some noise phenomena also exhibit a deviation from white noise at very low frequencies. This so called i/f noise or pink noise has a power spectra density that approximates a curve that inversely proportional to frequency. It can be dominant at low frequencies but drops below the flat thermal noise at frequencies ranging a few Hz to a few kHz, depending on the devices in question.6
Noise Power Spectral Density Graph
The following graph illustrates the power spectral density of noise from electronic components starting at a frequency of 1 Hz and extending to 1014 Hz for at a temperature of 290 K. Low frequencies display the 1/f effects, which are dominant until their power spectral density drops below that of thermal noise. Very high frequencies include quantum effects. The power spectral density can be considered flat for most of the frequencies over which electronic devices operate.
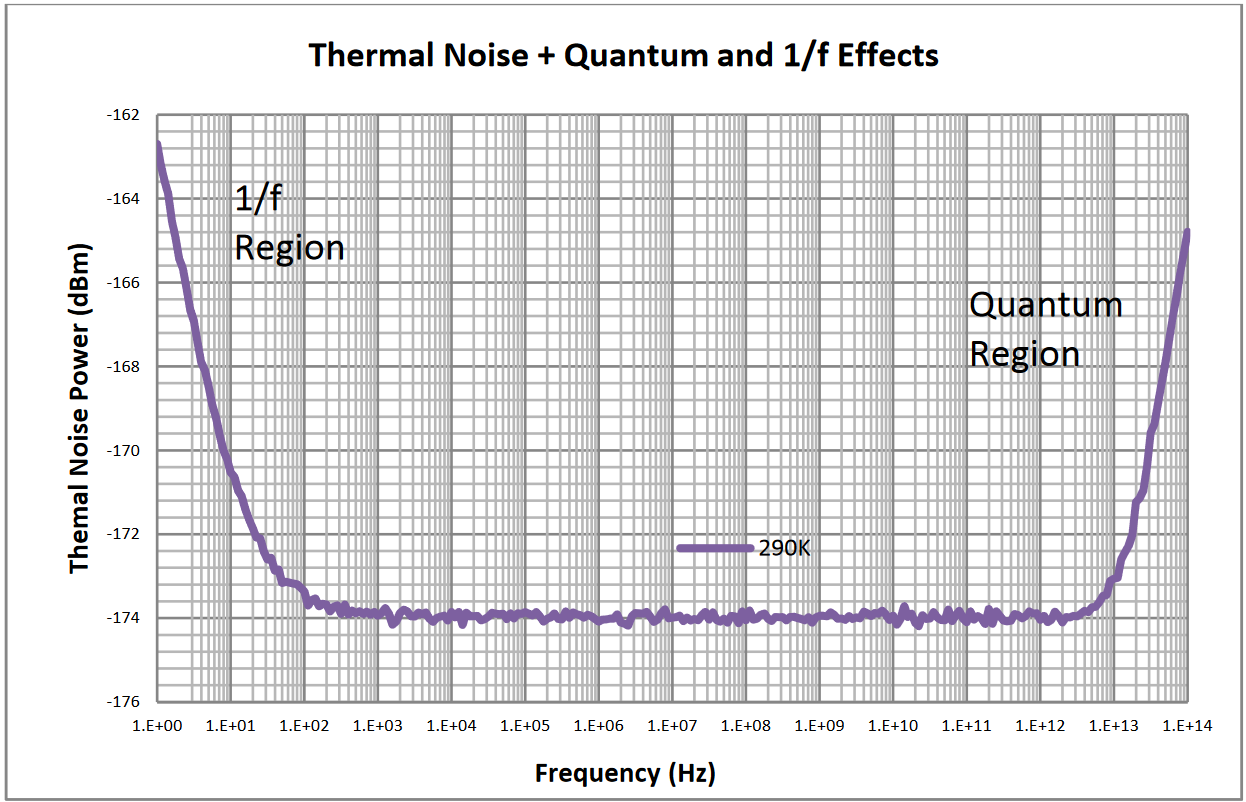
Noise in Electronic Components
All physical matter undergoes molecular vibrations as a result of thermal energy. Temperature is in fact a measure of the average kinetic energy of the moving molecules. Electronic devices are no exception. All electronic devices contribute noise at some level due to the vibration of molecules.
Resistors
Resistors contribute thermal noise caused by the random fluctuations of their internal molecules. It is often useful to consider the noise contribution of a resistor in terms of its equivalent noise voltage of its equivalent noise current. These values can be derived from knowledge of kits, the thermal energy of particles, also known as the thermal noise floor. The derivation for the equivalent noise voltage caused by thermal noise in a resistor is shown in Appendix 1. And is given by

The equivalent thermal noise current is given by

The noise power of resistors has a flat power spectral density and depends only on temperature and resistor value.
Capacitors
Ideal capacitors, like all reactive elements do not exhibit thermal noise. Capacitors, however, are made with imperfect conductors and dielectrics and therefore have an associated resistance. The noise voltage from a capacitor can be derived from the noise voltage of a circuit containing a parallel combination of a resistor and a capacitor. Letting the resistor rise to infinity gives us the thermal noise power emanating from the capacitor alone as shown in Appendix 1.

An interesting result occurs when we let the effective parallel resistor go to infinity. The total noise power integrated over all frequencies is only dependent on temperature and on the capacitance value.

Inductors
Ideal inductors, like all reactive elements, do not exhibit thermal noise. Real inductive components, however, have the losses in their windings and in their magnetic cores. These losses can be modeled as an equivalent series resistor, which can be show to contribute noise. Appendix 1 shows a derivation of the noise in inductors. It is only dependent on the effective series resistance of the inductor and is given by

Active Devices
Active devices can have many noise contributors. Each of its resistive elements contributes thermal noise. Bias currents contribute shot noise. The internal reactance of all circuit elements shapes the power spectral distribution of noise. It is often useful to model all noise sources in a circuit element in terms of an equivalent noise voltage and current as shown in the Op-Amp in Figure 10.
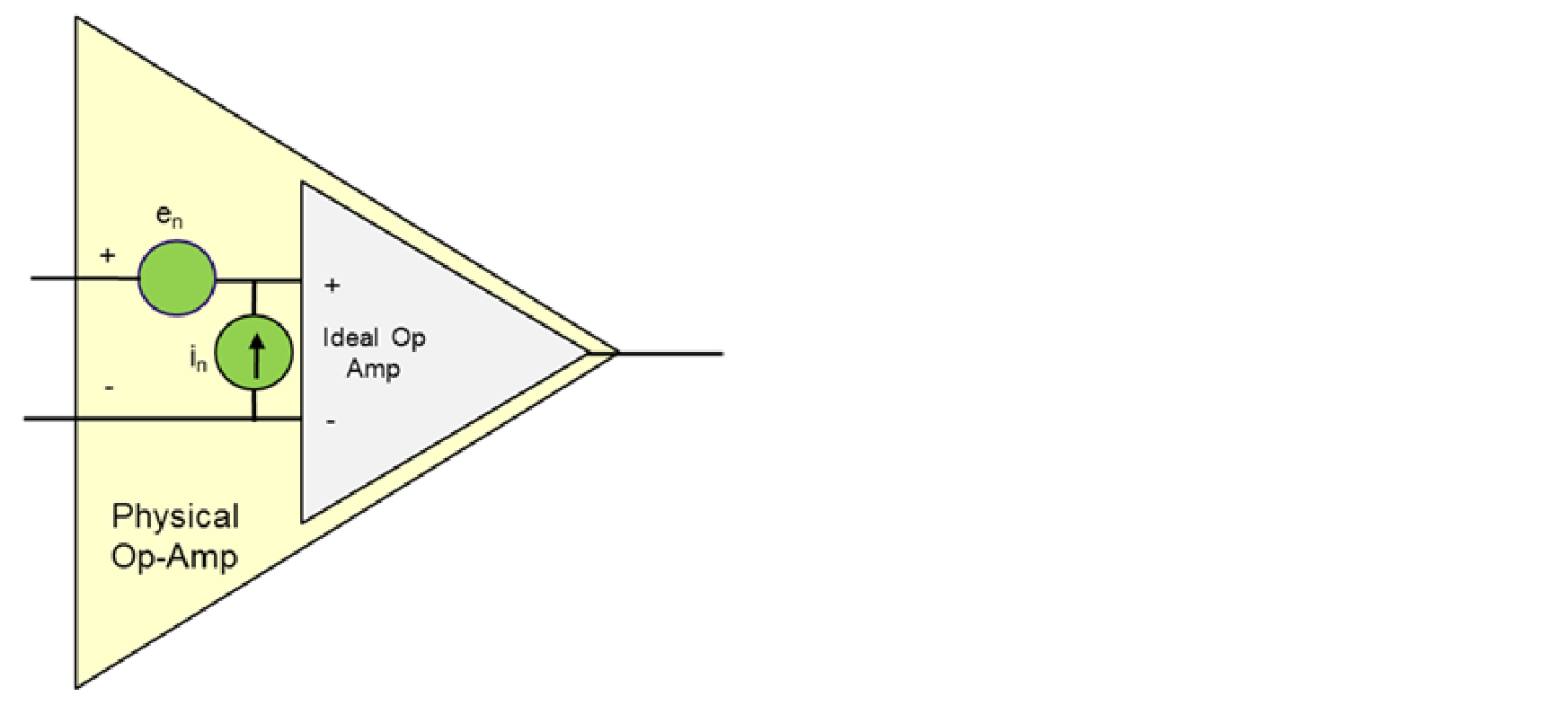
The real op-amp is modeled as an ideal noiseless op-amp with the addition of noise voltages and noise currents at its input. The noise contributions can also be modeled with equivalent noise sources at the amplifier output. The noise voltage and noise current represent the aggregate contributions of all the circuit elements inside the op-amp. Resistive elements contribute thermal. Bias currents contribute shot noise. Reactive elements can shape the noise power spectral distribution. Transistors, RF amplifiers and all active components can be modeled in this fashion. The actual values of the equivalent noise sources can be ascertained with measurements or with careful modeling of the internal circuitry of the amplifier.
Conclusion
Noise exists in all electronic systems. An understanding of noise and how to appropriately measure, model, and account for its effects in a system is an important concern in RF and microwave receivers that must extract information from extremely small signals. Noise added by circuit elements can conceal or obscure low-level signals, adding impairments to the signals being received.
Measuring the noise contributions of circuit elements, in the form of noise factor or noise figure is an important tasks for RF and microwave engineers. This paper, along with its associated appendices presents an overview of noise measurement methods, with detailed emphasis on the Y-factor method and its associated measurement uncertainties.
1 This paper assigns all added noise to the output of the amplifier. Other derivations exist where the added noise is modeled at the DUT input.
2 Friis, H.T., Noise Figures of Radio Receivers, Proc. Of the IRE, July, 1944, pp 419-422
3 Noise sources with a port impedance that changes between the “ON” and “OFF” states contribute additional errors to the noise figure measurement.
4 Agilent Application Note: High Accuracy Noise Figure Measurements Using the PNA‐X Series Network Analyzer.
5 Kerr. A.R and Nanda, J. P. 42
6 Johnson, J. B. (1925)
Find more valuable resources at TEK.COM
Copyright © Tektronix. All rights reserved. Tektronix products are covered by U.S. and foreign patents, issued and pending. Information in this publication supersedes that in all previously published material. Specification and price change privileges reserved. TEKTRONIX and TEK are registered trademarks of Tektronix, Inc. All other trade names referenced are the service marks, trademarks or registered trademarks of their respective companies.
8/2021 37W-30477-1


