Semiconductor junctions, from the millions of transistors used in integrated circuits to the largearea compound junctions that make high brightness LED's possible, are all susceptible to early failure due to increased heat. This becomes an even larger issue when feature size shrinks and current requirements increase. Even normal operation can cause heat build up, raising the junction temperature. These elevated temperatures can cause an increase in defects within the junction, which can lead to decreased performance, as well as a shortened lifespan. An accurate temperature-measurement method for the semiconductor device is needed to ensure that critically high temperatures are avoided. In this article, we will show how a simple junction-temperature measurement can be performed using common test and measurement instruments and how this information can then be used to monitor operating conditions for a given device.
Background
The ideal measurement of junction temperature is to monitor the device temperature as close as possible to the heat source. Current flowing through a semiconductor junction produces heat, which then flows through the junction material to the outside world. One method that could be employed is to place a temperature sensor very close to the semiconductor junction and measure the sensor output signal. As the heat flows to the outside area, it would cause a rise in temperature of the area and the sensor. This is straightforward, but there are physical limitations to this technique due to the finite size of the sensor. In many cases, the sensor itself would be larger than the junction to be measured. This would add a large thermal mass to the system, and additional error to the measurement which would lessen the accuracy of the measurement. Therefore, this technique would not be very useful in most applications.
A better technique is to employ the junction itself as a temperature sensor. With most materials, there is a strong correlation between the forward voltage drop of a junction and the temperature of that junction. The point at which a junction becomes nonlinear with respect to junction temperature is dependent on the material of the junction as well as its design. It is safe to assume linearity for most materials in normal operating environments up to 80-100°C. Nonlinearity can be determined experimentally by measuring the voltage at higher and higher ambient temperatures, until a deviation from linearity occurs
This relationship is nearly linear for most devices and can be expressed mathematically as:
Tj = m . Vf +To (Equation 1)
where
Tj = junction temperature in°C
m = slope* in°C/Volt
Vf = forward voltage drop
To = intercept* in°C
*Device specific parameters
So, at a given temperature, Tj , the semiconductor junction, will have a specific forward voltage drop, Vf . If we measure the Vf at two different temperatures, we can calculate the slope, m, as well as the intercept, To, for a particular junction. And, because this relationship is linear, we can then use equa tion 1 to find the junction temperature under different conditions simply by measuring the Vf . Knowing Tj for different operating conditions and packages allows us to calculate thermal parameters such as thermal resistance for differing package types and designs. This is important when designing for a particular operating condition by ensuring maximum lifetime for the device, because thermal effects are a major contributor to early device failure.
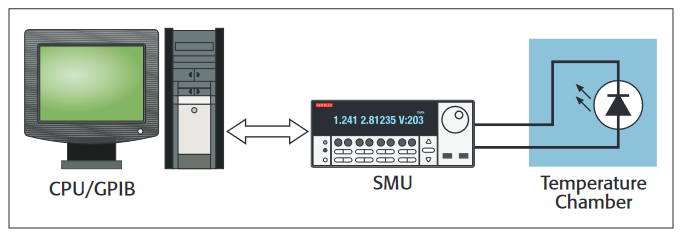
Test Technique
In this test technique, the device-under-test (DUT) is placed in a temperature chamber and connected to the drive and measurement equipment. This can be a programmable current source and voltmeter, but there are also instruments capable of sourcing a current and measuring a voltage simultaneously. They are commonly referred to as Source Measure Units (SMU's) and can simplify the instrumentation considerably. (See Figure 1.)
Next, connect the SMU to the device using a four-wire, or Kelvin, measurement technique. Four-wire voltage measurements decrease the error caused by lead resistance in a voltage measurement by sensing the voltage around the DUT, not in sensing it at the input to the SMU (see Figure 3 for a close-up of four–wire measurement).
Place the DUT into an environmental chamber and set the chamber to an initial temperature. The initial point is commonly measured at 25°C, with the DUT then allowed to reach thermal equilibrium. A dwell time can be determined experimentally, but, for most packages, a soak of 10 minutes should be sufficient
After the junction has come to thermal equilibrium, a short duration current is sourced into the DUT and the voltage drop is measured. The time duration of the pulse as well as the amplitude are very important. Delivering a larger amount of power (too much current or too long a pulse) may skew the results by heating the junction. Many times, the junction under test is a silicon or compound diode. For these device types, a good starting point for experimentation is 1ms of sourced current at a few mA of drive current. If you are unsure, the self-heating of the junction can also be determined experimentally by using a source capable of very short pulses (<1ms). You can then experiment by varying pulse widths and compare the voltages of each pulse duration. Voltage differences on the order of 1–2mV commonly indicate a 1°C change in junction temperature.
This measured voltage is the Vf1 @ Tj1 (25°C).
The temperature is then elevated to a higher value (50°C for example), the DUT is allowed to reach thermal equilibrium, and the current pulse is again delivered. Voltages recorded at this temperature are labeled the Vf2 @ Tj2 (50°C in this example).
These steps can be repeated over a number of values and then plotted as Voltage vs. Junction Temperature (Figure 2). It is best to use at least three temperatures in the analysis to check for any discrepancies in the approximation.
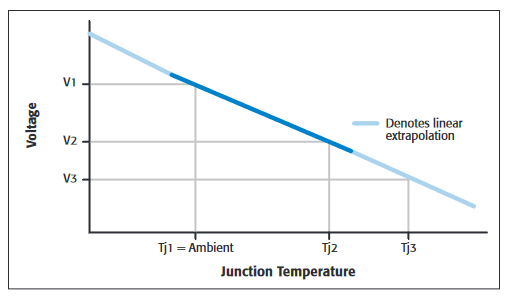
You can now calculate the slope, m, of the line as well as the intercept
Equation 2: Calculating m (Point-Slope form of equation 1)
Tj = m · Vf +T0 (Equation 1)
Tj2 – Tj1 = m(Vf2 - Vf1)
(Point-Slope form of equation 1)
m = (Tj2 – Tj1)/(Vf2 –Vf1)
and you can then calculate T0 by extrapolation.
Tj2 – Tj1 = m(Vf2 – Vf1)
(Point-Slope form of equation 1)
By setting Vf2 to 0, equation 2 becomes
Tj2 = Tj1 – mVf1
Tj2 in this case is equal to the intercept, or T0.
T0 = Tj2 = Tj1 - mVf1.
Real World Example: High Brightness LE
In this example, a new high brightness LED die is being developed. This new device is designed to carry more current than previous units, and we need to be sure that we can keep the heat flux high in order to minimize the junction temperature. This will ensure that we have adequate device lifetime for some of our more rigorous applications. A common LED failure occurs when the bond wire connecting the Anode or Cathode to the LED Die is broken. The common cause of breakage is temperature cycling of the bondwire. This is a direct result of elevated junction temperatures due to inadequate heat removal.
We place the LED die in an oven and follow the above prescribed test plan. We measure the following results:
Vf1 @ Tj1 (25°C) = 1.01 V
Vf2 @ Tj2 (50°C) = 0.78 V
m = (50 – 25°C)/(0.78 – 1.01)V
= –108.70°C/V
T0 = Tj1 – mVf1
= 25°C – (–108.70°C/V)*(1.01V)
= 134.79°C
So, the first order equation describing the Junction Temperature vs. Forward Voltage for this device is
Tj = –108.70°C/V · Vf + 134.79°C
We can now vary other aspects of the evaluation such as operating current, environmental/case temperature, and packaging, and simply measure the Vf to measure the actual junction temperature.

Sources of Error
The largest source of measurement error comes from the uncertainty of measurement of temperature in the environmental chamber. This measurement is typically made using a thermocouple, which can have errors of ±2° or more. Additional accuracy can be obtained by placing a more accurate thermal measurement sensor, such as a thermistor or RTD, near the DUT and using a separate DMM to measure the temperature.
Uncertainty in the voltage measurement also adds to the error in the calculation of junction temperature. Selecting an instrument with a high degree of accuracy and resolution on voltage measurements is the key to minimizing this error.
Errors in the junction temperature measurement can propagate to other thermal cal culations, such as thermal impedance and resistance as well. Therefore, minimizing these errors is critical to obtaining accurate measurement results
Conclusion
A simple electrical technique for measuring the junction temperature of a semiconductor junction was shown. The data can then be used to analyze the effects of heat sinking, environmental, and source conditions on the junction in question.
Find more valuable resources at TEK.COM
Copyright © Tektronix. All rights reserved. Tektronix products are covered by U.S. and foreign patents, issued and pending. Information in this publication supersedes that in all previously published material. Specification and price change privileges reserved. TEKTRONIX and TEK are registered trademarks of Tektronix, Inc. All other trade names referenced are the service marks, trademarks or registered trademarks of their respective companies.
No.2681 0206

