Introduction
The need for seeing faster time-varying signals
As faster time-varying frequency signals become more widespread, Tektronix has responded to the need to provide more visibility of very short-time events with Real-time Spectrum Analyzers (RSA) employing short Discrete Time Transform frames that can be fully overlapped.
This primer discusses the needs and analysis benefits of this technique, explores how it works, and how it can be used most effectively to see time-varying RF signals with greater clarity than ever before.
Various terms for these Time-to-Frequency Transforms are in common use. Fast Fourier Transform (FFT), Discrete Fourier Transform (DFT), Discrete Time Transform, and Chirp-Z Transform (CZT) are all used in this paper. The term, Discrete Time Transform, is used here as the generic term. FFT and CZT are used when the specific transform in use is important to the performance of the measurement being described.
Expand the Spectrogram View
A Spectrogram is a display of multiple signal spectra. Each spectrum (a normal RF spectrum display) is placed at the bottom of the spectrogram as a single line. The frequency scales is still the horizontal axis, but now the amplitude information is converted to color, or intensity for the single line. The next spectrum is placed under the previous one, and the whole display is shifted up by one line.
As this continues, the display vertical axis becomes the "time axis", and the three dimensions of the signal are all visible:Frequency, Amplitude and Time.
Overlapping transforms works somewhat like a "zoom" for the Spectrogram. It does this by effectively stretching the time scale. While adding overlap to a Spectrogram does indeed overlap small time events, it enables much greater visibility of frequency changes with time.
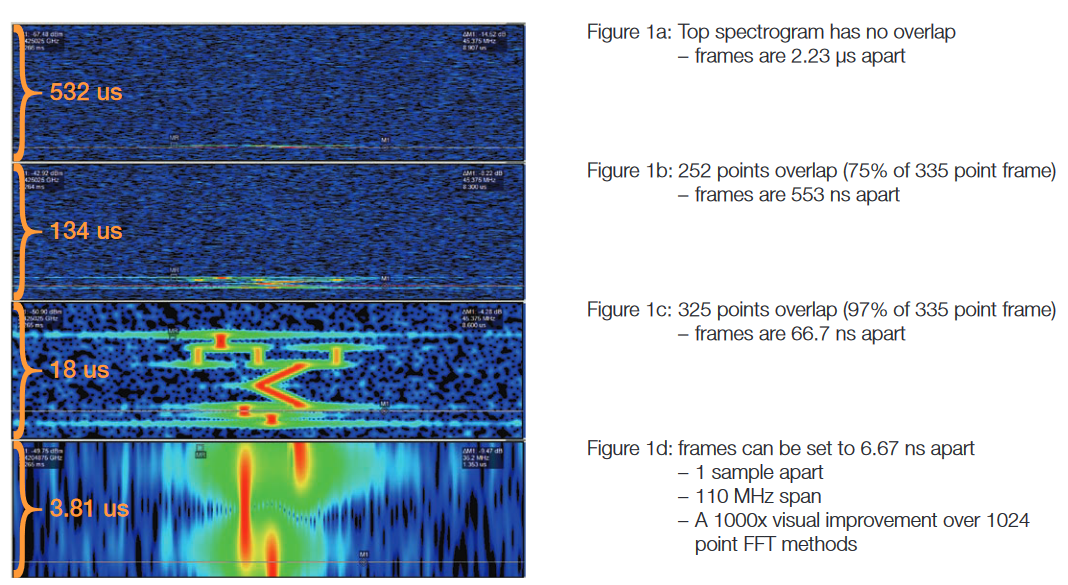
Figure 1 shows four separate Spectrograms of the same signal with increasing amounts of overlap. Figure 1a has no overlap, and the incoming signal has a short enough duration (10.5 μs total) that it occupies less than 5 spectrum frames.This is not enough to see even the general nature of the time variations within this signal. The second Spectrogram, Figure 1b, has a 75% overlap, which gives a vague visibility of the time-varying signals.
The third Spectrogram, Figure 1c, has a 97% overlap and provides an excellent view of the multiple signals sequenced within this 10.5 μs pulse. A CW hop, then three frequencies simultaneously in the second hop, then a down-chirp followed by an up-chirp, and finally two more frequency hops. The final Spectrogram display, Figure 1d, is fully overlapped, with only one sample separation between the start time of sequential transform frames. This gives a greatly expanded view into the last two frequency hops.
How Overlap works
Overlapping many Time-to-Frequency transforms
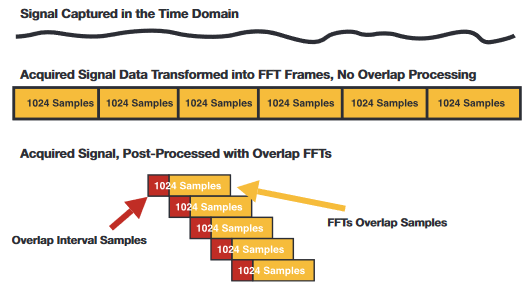
Early Real time Spectrum Analyzers (RSA) processed the data from the A/D converter mostly in a straight sequential manner. The first 1024 bytes went into the first FFT (first frame), the second 1024 bytes into the second FFT (second frame), etc.This method of viewing time-varying signals has a fundamental limitation. The amount of time required to digitize all the samples of the input signal required to fill one FFT frame defines the shortest resolvable time event. Each FFT frame is displayed as one event in time. If multiple events occur within the time of one FFT frame, they will all appear to happen simultaneously.
One method of gaining shorter time-visibility is to use an alternate Discrete Time Transform method. The mathematics of an FFT requires that the number of samples used must be an exact power of 2. Also, the FFT requires that the number of time samples in the input frame must be the same as the number of frequency samples, or bins, that will be contained in the spectrum output from the FFT. A very common frame length is 1024 points.
There are some Discrete Time Transforms that are not as limited as the FFT. One such alternative is the Chirp-Z Transform (CZT). The CZT can provide 1024 output points with only 200 or 300 input points and under some conditions may be useful with as few as 12 or 13 input points.
The visibility of events occurring faster than a frame length in time can be greatly enhanced by overlapping multiple Timeto-Frequency transforms. The same string of digital samples of the incoming analog signal is used, but instead of simply chopping it into sequential frames, the incoming samples can be placed into frames such that, for example, the samples starting with number 1 to 1024 are placed into frame one, then samples 512 to 1536 are placed into frame two, samples 1025 to 2048 are placed into frame three, and so on. In this manner each frame has 1024 sequential samples, but the first half of them are shared with the previous frame, and the last half are shared with the subsequent frame.
For the display of a spectrogram containing more spectrum lines than the spectrum analyzer display can separately show, there is a display compression algorithm used which combines groups of spectrum lines into one display line. The current Tektronix RSA method is to select a Scale value which compresses these spectrum lines by a power of two. If the Scale is "0", then no compression is used. For a Scale of "-2", the lines are compressed in groups of two lines into one display line. For a Scale of "-4", the lines are taken in groups of 16 and compressed into one display line.
This same Scale control is used to set the amount of overlap employed, which will therefore appear to be a zoom control for the spectrogram display. If the Scale is set to "1", then the spectrum lines will be zoomed by a factor of 2, which means that the Time Transforms are overlapped by 50%.The first half of each frame is shared with the last half of the previous frame, and the last half is shared with the first half of the subsequent one.
If the Scale control is set to "4", then the is overlap is 94% from one Transform to the next. When the Scale reaches the setting where there is only one sample at the beginning of each frame that is not shared with the subsequent one, then no further zoom is possible. Since the CZT can use a different number of input samples depending on analyzer settings such as capture bandwidth (Span), Resolution Bandwidth (RBW), type of windowing filter, etc., the maximum Scale setting available will also be dependent on these analyzer settings.
The length of frame in use at any time can be discovered by selecting the Analysis button as shown in Figure 2, and then the Spectrum Time tab in Figure 3. The length of the spectrum frame is available in this control. To find the number of samples in this frame, select the Acquisition button, and the Sampling Parameters tab. Here both the current sampling frequency and sample time are listed as shown in Figure 4.
When the Scale is set to a value greater than "0", this means that each Discrete Time Transform spectrum is displayed, it contains some information from the previous spectrum.
An example of a 94% overlap transform processing could be demonstrated by a 279 sample frame with 262 samples overlapped from each frame into the next. At a 12.5 MHz sample rate, each spectrum frame would occupy 23.76 μs.Each spectrum would start 1.36 µs (17 samples at 80 ns per sample) after the previous one and could show a 10 MHz span. Narrower resolution bandwidth (usually the result of selecting a narrower span) would result in each spectrum taking up more time, while simultaneously resolving frequency components that are closer to each other, while wider spans are the opposite.
With this overlap technique, a very short spectral event (particularly one that does not even last as long as one frame) can be seen (even if at reduced amplitude) in many sets of spectra that are displayed adjacent to each other.
The advantage this provides is visibility of the very-short time variations that may occur within a signal. The disadvantage is that since the transform frames are overlapped in time, the various frequency events will also appear in the Spectrogram display to be overlapped by this same amount. This effect will prevent relative timing measurements between spectral events from enjoying an increase in timing measurement resolution, even as the spectrogram gains in visibility.

Spectrum and Spectrogram comparisons
Non-overlapped transform processing
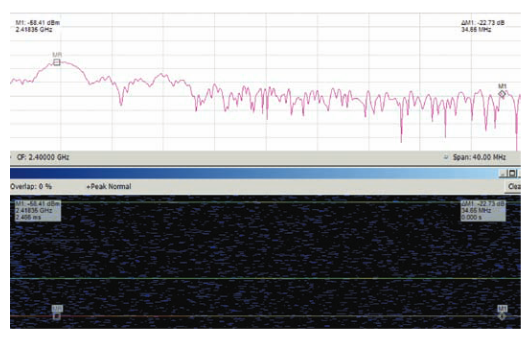
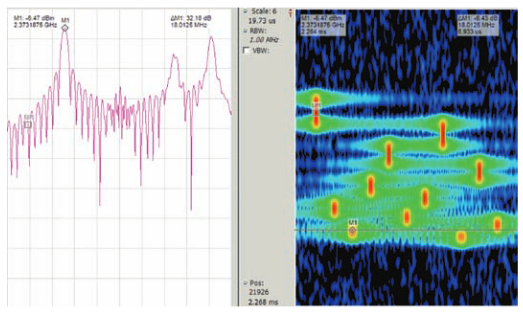
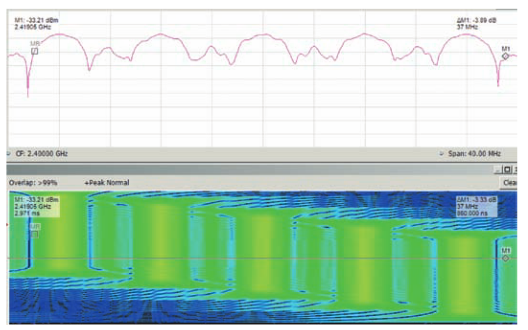
Figure 6 shows the spectrum and spectrogram that includes a radar pulse. This pulse is frequency-hopped with five steps across 32 MHz. When all five hops are included, it is 2 µs long.Using a 40 MHz span, this is just about 1/4 of one transform frame spectrum frame of 7.460 µs. Each hop lasts only about 1/20 of one frame.
Therefore, it exists in one frame only, and detail can not be seen without overlap processing. The spectrum plot that is displayed is randomly "skewed" to one side or the other due to the random position within the frame where the pulse happens to land.
It is difficult to trigger such a narrow pulse and reliably position it in the middle of the FFT frame, and even this would not produce a useful Spectrogram display.
Overlapped time transform processing
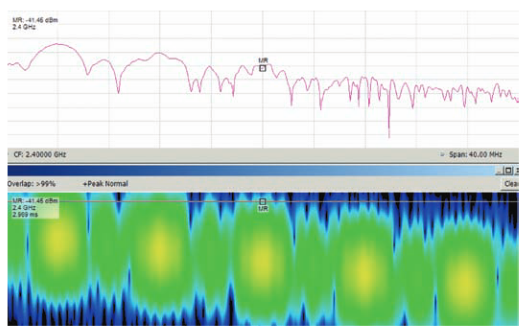
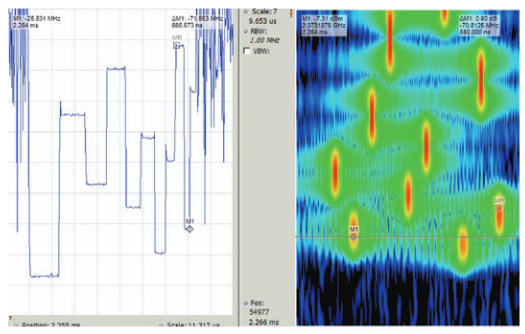
In Figure 7 the RSA using 40 MHz bandwidth shows this same hopped pulse using overlap time-transform processing where the frame-to-frame time interval is reduced from 373 samples (no overlap) to 1 sample with 372 sample overlap. The result is dramatic. Even though the pulse is still shorter than one frame, the individual frames are sequentially positioned 20 ns apart. This clearly shows the steps that are increasing in frequency throughout the pulse, and the approximate time of each step.
Stretching time and impact on Spectrum view
The effect that overlapping really brings is not really a “zoom”, but is much more a “stretching” of time. This gives much improved visibility of time-variant phenomena, but the events are all stretched out together. Not only do the Time Transforms themselves overlap, but the spectral events themselves are now overlapped in the display.
In Figure 8 the marker is placed at the beginning of the middle hop of the pulse. Note that due to the overlap of the frames, the individual steps appear to be largely concurrent in time. this overlap is not real, but is due to the fact that as the frames overlap, each one contains many samples from other frames, both before and after itself.
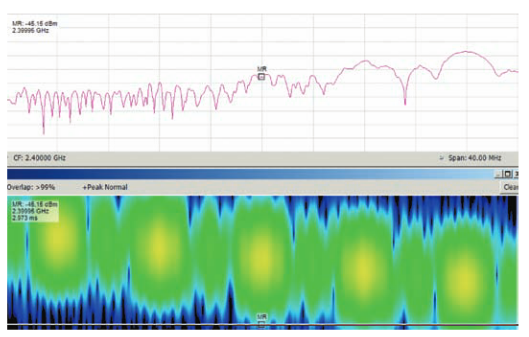
Figure 9 shows the marker placed at the end of the same middle hop. These pictures clearly show the frequency and time-varying nature of this pulse, which is entirely within the frame time of one transform. This visibility would not be possible without overlapping adjacent frames.
The effect of stretching time has made all of the hops of this pulse appear to mostly be concurrent in time, even though these hops are all separate in time. One of the biggest contributors to this effect is the fact that this particular pulse contains five sequential events, and the entire collection, at 2 μs long, is one quarter the length of one (7.46 μs long) transform frame.
The discrete time transform process is not an infinitely short slice of time. It requires processing multiple cycles of the input frequencies in order to separate them from each other. Therefore, if there are several different frequencies that are all within this frame, they will all be reported by the transform. The output will create only one spectrum. Therefore, even if these frequency hops are all separate in time, they will all be displayed together in the one spectrum if they exist within the one time frame.
Example: a pseudo-random modulated pulse
Here is an 8.3 μs long radar pulse with internally hopping frequency. The hopper changes both frequency and duration with each hop segment. This is seen in Figures 10 and 11. The duration of each hop is shorter than the previous one.
As the hop durations become shorter, the time-overlap effect of the overlapped transforms makes it even more important to use the Frequency vs. Time display to measure the actual timing of the hops.
The Frequency vs. Time display can be paired with the Spectrogram. This allows markers to be used to measure the timing of events without the stretching effect.
Note: These measurements were done using the 10% and 90% voltage points on an RF pulse.
Spectrogram Risetime
Another effect that limits the ability to actually increase the time-resolution in Spectrogram is an apparent “risetime” imparted to the spectrogram when using overlapped transforms. This also increases the apparent time-overlapping of the separate hop segments of the 5-hop pulse.
For signals that have duration longer than the transform frame time, the risetime is dependent on the Resolution Bandwidth Filter in use. This filter has a risetime, and this is the primary component of the Spectrogram Risetime. The overlapping simply makes this component of signal risetime more visible.
For signals with duration less than one transform frame, the risetime becomes more dependent on the Time Window in use. Both of these signal conditions will be discussed.
Risetime due to Resolution Bandwidth (RBW)
Spectrogram Risetime is also dependent on the selected span (which determines the actual effective sample rate used and therefore the default selection of resolution bandwidth filter used). This component of the risetime is not dependent on the amount of transform overlap. It is dependent solely on the RBW filter in use at the time. The filter can be selected manually, or automatically based on the selected span and its resultant effective sample rate. This component of the risetime predominates when the signal duration is significantly longer than one transform frame.
Note that there is also an equivalent falltime and time smearing that occurs at the trailing end of a pulse or other frequency event. Both ends of a pulse have the same effect applied to them.
Measuring the Spectrogram RBW Risetime
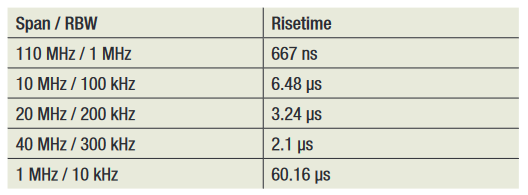
The table shown in Figure 12 gives the results of a sampling of actual measurements with different RBW settings.
The RF pulse used here was 90 µs in duration. This ensured that only the risetime of the RBW filter was being measured.
This risetime limits the time resolution available when attempting to measure the timing of any spectral events using the spectrogram.
When the event being measured is shorter than one time transform frame (usually CZT), then the primary contribution to the apparent risetime variation will be the smearing from overlap.
RSA time overlap
For an example of the 40 MHz acquisition bandwidth (40 MHz Span) with other timings in the Auto mode, the effective sample rate is 50 MHz (20 ns per sample). Each CZT transform requires 373 samples, resulting in each frame being 7.46 μs long. When using non-overlapping frames, each spectrum is produced from the next frame that consists of 7.46 µs of data. (373 samples times 20 ns per sample). Therefore if a signal were to be turned ON just at the joint between two sequential frames, it would contribute no energy to the first frame, and fully contribute to the next. This implies that using the spectrogram, time events can be measured with a “resolution” of 20 µs.
One might be tempted to extrapolate that if the fully overlapped frames were used (such that the time between the start of one spectrum and the start of the next one is 20 ns – one sample), that the time resolution would be 20 ns, but it is not.
Some understanding of the process may help to be aware of the pitfalls.
FFT Window Effects on Time Resolution
When using 40 MHz span, the A/D converter is continuously digitizing at a 100 MHz rate which provides both I and Q samples at a 50 MHz effective rate (and filling up the memory - a record). Each Chirp-Z Transform (CZT) will be provided with 373 contiguous samples from somewhere within the stored record (a frame). In the example, a 40 MHz span was selected with a frame 7.46 µs long.
Consider the following specific example of what happens with overlapped frames. If the first frame observed is the last one before a short burst of RF, this frame has no power contribution from the RF burst since the burst has not yet started. The second frame is overlapped by 372, and therefore starts one sample point later. It contains only one sample point of power from the burst. Each subsequent frame will contain one more additional sample of the burst until finally there is one frame that contains the entire burst (if the burst is shorter than a frame), or until there is a frame that is entirely filled with the burst (if the burst is equal or longer than the 7.46 µs of a frame).
Because each frame contains more power than the previous frame, the second frame under examination can, at most, contain 1/373 of the possible full power of the burst. This is in fact explained by Parseval’s Theorem, which states that a discrete transform will produce a spectrum that displays the power level of a coherent signal that increases in direct proportion as the square of the number of samples of that signal which are included in the Transform frame. The formula is:
Power(dB)=20 Log(SignalSamples / TotalSamples)
Amplitude effects are discussed separately in more detail.
There is a second effect due to the time window. This reduces the amount of contribution that the samples at the ends of the frame are allowed to make to the spectrum (reduces to essentially zero at the very end samples). The purpose of this time-filter is to eliminate the end effect of having an abrupt start and/or an abrupt end to the signal that is in the frame, due to the frame ending. This window further reduces the contribution from the signal that is seen when any portion of that signal is present near one end or the other of the frame (previously demonstrated in Figure 8 and Figure 9). The apparent horizontal smearing observed in the Spectrogram is a simple overlay of the individual sin x/x of each of these short duration pulses as seen in the spectrum view.
These two effects together mean that the first spectrum that contains the one sample of the burst will essentially have no spectrum of it. The next spectrum will have very little more. It is not until there is a spectrum that is nearly one-quarter full with the burst that there is a significant percentage of the amplitude of the burst displayed.
This slows the effective risetime of the Spectrogram, and its resultant time resolution.
Overlap risetime and the effects of different window filters
When displaying pulses that are shorter duration than the time transform frame, the apparent spectrogram risetime is a strong function of the time window selected for use by the CZT. Since the transform window is a large part of the risetime limitation when using the spectrogram for short pulses, the effects of removing this filter are examined. One of the available filter selections is Uniform. Like having no filter at all.
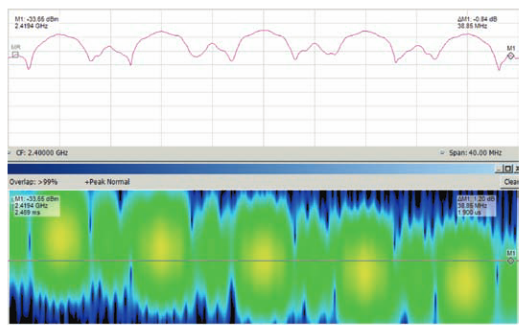
Using the default Kaiser window, shown in Figure 13, all of the frequency hops are reduced in apparent duration and show a slow risetime due to the window filter. The RF hops as generated are actually 400 ns duration each, and have a risetime essentially that of one half cycle of the RF frequency (2.4 GHz - about 200 ps).
The Spectrogram shows about 4.9 μs for each segment length, but the length should be 373 samples for one frame worth of samples, plus 20 samples for the actual length of the segment, or 7.860 μs. The reduced stretched length is due to the Kaiser window. The apparent risetime is about 1.48 μs as measured with the same method used for the risetime table values in Figure 12.
Removing the filter can be expected to improve the apparent Risetime of the Spectrogram. But there will now be the effects of the abrupt ends of the frame. Figure 14 shows the result using the Uniform window on the same signal.
The start and end of the individual hops are still overlapped in time. This is unavoidable with overlapped transforms. But now Figure 14 has a much more crisp beginning and end of each segment. Compare this to Figure 13 – the default window. With the use of the Uniform filter the effective Risetime has indeed become faster. While for 40 MHz span with the Kaiser filter the risetime was 1.48 µs, the Risetime obtained with the filter removed is now 320 ns. This is almost five times faster.
The stretched length is now as expected. Since the CZT with the Uniform filter uses only 149 samples for one frame, the length should be 149 samples for a complete frame, plus 20 samples for the segment itself, should be 3.380 μs. Figure 13 shows 3.3 μs. This is very close to the expected stretched length.
Uniform filter artifacts
When using the Uniform window, the time-varying hops are more visible, but the artifacts from the edges of the hops are now quite apparent. They will cover up any small signals that might be near the main ones. In fact the end effects of any one of the hop segments show up as significant moiré patterns in the Spectrogram.
The end effects are formed due to the pulse effectively starting a frame only when that frame includes some samples of it, and ending when the pulse itself ends. Without the window filter, this means that as you move through the overlapped frames, you will see a sharp narrow pulse in the first frame, and a slightly wider pulse in each subsequent frame until the entire pulse is within one frame. As each frame analyzes the slightly wider pulse than was seen by the prior one, the sin x/x pulse spectrum changes its periodicity and the pattern is formed in the Spectrogram.
On the other hand, without the filter, all of the frequency components of this hopped pulse are time-stretched into one frame without any one frequency being reduced any more than any other. They are all equally reduced by the shortness of the pulses. And the overlapped frames allows the selection of a window exactly in this time position. The upper spectrum view in Figure 14 shows this, with all of the hop components shown at equal amplitudes instead of being tilted.
Note: While the edges are more clearly delineated in Figure 14, the time smearing might lead one to incorrectly conclude that the discrete hopping pulses where ON at multiple frequencies at the same time.
Measuring Time Events Accurately
There is a method to accurately measure time within very short time-varying RF signals. The RSAs are optimized to correctly measure time-varying phenomena. Simply use the Time versus Frequency display or demodulation modes.
The RSA also has multi-domain analysis. The same stored time record of samples can be processed simultaneously by several different demodulation and measurement software routines. This is the preferred method for accurate measurement of the time-variations. For this frequency-hopped pulse, the Frequency versus Time (FvT) display is used.
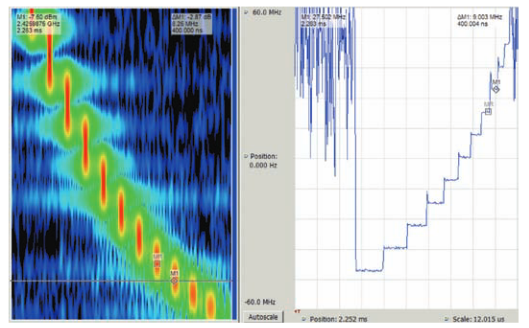
Figure 15 shows a radar pulse that internally is composed of 11 sequential frequency hops. This shows both a Spectrogram view, and a FvT view. When display decimation is turned OFF, the FvT display uses the full sample rate to measure frequency at each RF sample. In this example, the span is 110 MHz, so the complex (I/Q) sample rate is 150 MHz, for a complete frequency measurement every 6.667 ns. The sample rate defines the resolution of time measurements when using an FvT display.
The markers can be used on the FvT display to measure both frequency and time.
Multi-Domain Analysis
Figure 15 shows the Frequency versus Time display in the right window. Delta markers are placed at the transition points of a single hop portion of the pulse. The readout shows the hop time of 400 ns.
Since they are placed on the corners of the steps, the markers will also accurately measure the 9.003 MHz frequency step size.
The markers are correlated across both displays, so that each marker measures the same point in both domains.
Limitation of FvT measurements
There is one case where a Spectrogram is required and FvT can not make the measurement. As with other frequency discriminator type devices, the FvT measurement can not properly respond if there is more than one frequency present at the same time.
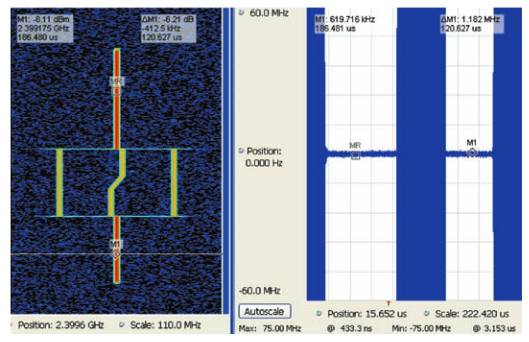
The Spectrogram (Figure 16 on the left) shows an initial single carrier, then a section with three carriers, followed by a final single carrier. The center of the three parallel carriers has a segment in its middle where the frequency ramps lower and then stays low.
The FvT display has no trouble showing the single carriers (note the markers placed one per carrier), but the middle section with the three simultaneous different-frequency signals has only wideband noise. This is very similar to the portions of time before and after the signal is present at all. The Spectrogram is required to see the nature of such a signal.
Amplitude Effects
Brief pulses
As previously mentioned, pulses or other RF events that have a duration of less than one FFT frame will be converted to spectrum information at reduced amplitude. The reduction is proportional to the amount of the time transform frame that such signals occupy. (Parseval’s Theorem).
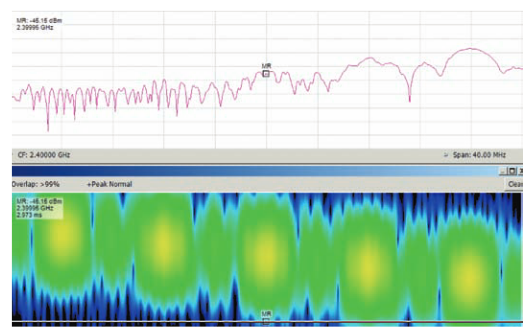
In Figure 17, the Spectrum that is produced by the one transform that contains the pulse is clearly varying in amplitude. The upper-most frequency shows as about -26 dBm, the next lower one appears to be -31 dBm, the next two are -41 and -47 dBm, and the last one is not even visible below the noise.
Yet all of the hop segments were generated at the same RF amplitude. The overall amplitude reduction is due to the individual segments being shorter than one transform frame.
The amplitude difference between the separate segments is due to their position within the time window filter (position in the frame.) Since the pulse was completely asynchronous to the frame, the one which was measured happened by chance to be located near the beginning of the frame. Therefore the first hop (the lowest frequency one) was severely reduced due to the window function applied to the CZT. This reduction becomes less as the hops occur later in the frame, and therefore closer to the middle of the window function.
These tables have correction values for several short pulse lengths. For both tables a bandwidth of 40 MHz is chosen. This bandwidth uses a transform frame length of 7.46 µs when the Kaiser window is selected and a frame length of 2.233 µs when the Uniform window is selected. Pulse lengths that are equal to or longer than the frame time will be measured correctly for amplitude. This table lists the errors that will cause reduced amplitude to be reported for short pulses.
The calculations used for this table assume that the pulse is centered in the frame, that the window used is either none, or Kaiser as noted in the column heading.
Another assumption is that there is no scalloping error due to the incoming signal being a different center frequency than the analyzer is tuned to. This can cause a few tenths of a dB additional error.
When using an FFT or other Discrete Time Transform, there is an amplitude variation effect commonly called scalloping. This is the result of the input signal landing either in the exact center of one of the FFT output bins, or landing somewhere in between two bins.
This effect can be easily understood if one views the result of the FFT as a parallel bank of many narrow filters. If the incoming signal slowly sweeps across the frequency span covered by the FFT, then when the incoming signal is exactly centered within one of the FFT output bins, the measured amplitude will be at its maximum. But as the incoming signal moves to a slightly different frequency during the next FFT, it will be slightly offset from the center frequency of the original output frequency bin. Eventually it will move enough so that it is centered in the next adjacent bin and will again be at maximum amplitude.
The minimum amplitude will occur when the incoming signal is positioned exactly between two adjacent FFT bins. The amount of amplitude reduction is dependent on the window function and the parameter of that window as used for the FFT, as well as the spacing between the output bins. The exact calculation of the maximum amplitude variation is beyond this discussion, but it can be as much as several dB.
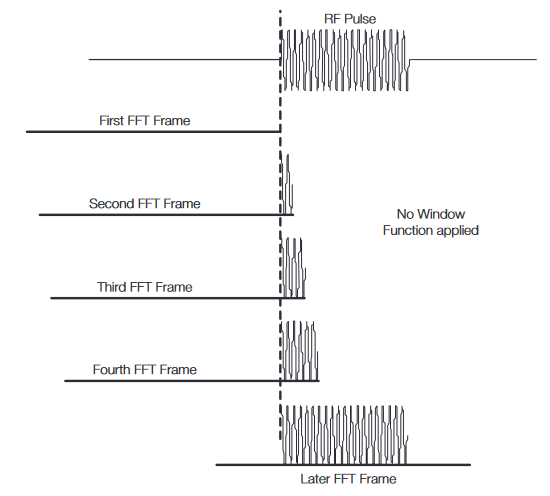
In Figure 19, there is a pulse of RF at the top. Beneath that the drawing shows four lines that represent four sequential overlapped frame times. Each of these frames is further along, and contains more of the RF pulse.
It can be seen that the power contained in each frame is more than the frame before. Then at the bottom is a frame (taken considerably later in time) which contains the entire pulse in its middle section. This frame will show the amplitude of the pulse the highest as will be seen in any of these frames.
These transform frames do not have any window filter in use.

Figure 20 has the same pulse and transform frames with the addition of a time windowing filter. This shows the much greater reduction in pulse amplitude which results from the pulse being at one edge or other of the filter, while the amplitude of a pulse in the middle of a frame will be only slightly reduced.
The correct amplitude will be measured for an RF signal which is equal to or longer than one frame, and is continuous throughout the frame. The amplitude reported by the transform process is normalized to the response of the filter used for the window function.
The Kaiser Window
The default time window for processing spectrum view and spectrogram in the RSA6000 Series is the Kaiser window. Figure 21 is a plot of the normalized response of such a filter.
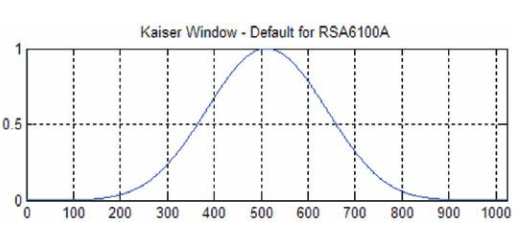
If the transform were to be performed on a frame of input samples without this filter, there would be spectrum artifacts generated due to the sudden start of the spectrum and also due to the sudden stop at the ends of the frame. The solution is to use this filter (or a similar filter) to reduce the response from the ends of the frame to zero. Then also to gradually increase the contribution of the samples that are nearer to the middle of the frame. The horizontal axis of this example plot is a frame of 1024 samples (although the shape is the same for any arbitrary number of input samples).
The amplitude difference between the filtered frames and the unfiltered frames for the table of pulse width versus displayed amplitude is derived from this plot. (See Figure 18).
Calculating Amplitude Reduction
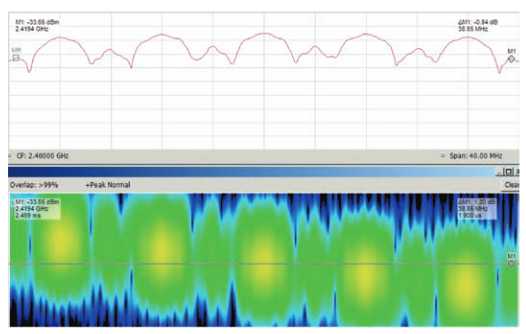
Figure 22 shows the use of overlapped transforms, where the marker position is in about the middle of the stretched display. The spectrum is the result of a transform where the entire pulse, with several frequency hops, is centered in the frame. All of the frequency hops are contained within the single frame. They are centered in the window function applied to the frame.
They all read between -15 dBm and -18 dBm.
Since each hop is 400 ns long, and the full frame is 7.46 µs long, the power recorded in the Spectrogram is reduced by Parseval’s theorem. The calculation is 20*Log(0.4/7.46) = -25.414 dB. There must also be an accounting for the correction that the power readout for the 7.46 μs frame already has due to the time window filter (Figure 21 Kaiser filter response) = +10.344 dB, for a total of -15.07 dB.
When a window function is used within an FFT calculation, the contribution to the spectrum result is reduced for samples which are nearer to the beginning and the end of the FFT frame. The samples at the end are reduced to zero. If the signal is continuous throughout the FFT frame, the calculated signal amplitude will be reduced by this reduction in the amplitude of some of the time samples.
Therefore the amplitude of the resulting FFT is corrected so that the reported amplitude of any signal is increased for this amplitude loss. This correction is done within the standard FFT math routines. The dB value required for the correction is nown for each time window function based on the cumulative reduction in sample amplitude. A simple calculation can be done by summing the normalized values of the window function and dividing by the number of samples in the frame. Then the dB value is 20*log(average sample reduction). For the particular Kaiser window used in this document, the correction is 10.344 dB.
The readings can now be manually corrected for narrow pulse amplitude. The center pulse reads -15.05 dBm and the correction is to make up for a reduction of 15.07 dB. The corrected amplitude for this pulse should be +0.02 dBm. When this pulse was increased to be longer than a transform frame, it measured -0.38 dBm. This is very close agreement between the practical measurement and the theoretical calculation (only 0.4 dB). Especially when you consider this amplitude measurement includes all distortions resulting from such a short-duration pulse.
Calculating amplitude correction for pulses that are not centered in the window is beyond the scope of this document, as it requires using the Kaiser curve separately for each side of the filter.
Other windows
There are several different windows available in the RSA Series. This document has explained the issues with the Kaiser and the Uniform windows. Other windows (such as the Blackman-Harris) will have greater or lesser time and amplitude effects than the default one. If you are using one of these others, you will need to re-calculate the amplitude and apparent spectrogram risetime effects.
The selection of the best window function for a particular signal is a subject beyond this paper, and is dealt with elsewhere in RSA documentation.
Super-short pulses
Pulses which are very significantly shorter than one CZT frame may not be visible at all either on the spectrogram, or in a spectrum view. Such pulses can only be triggered by the power trigger, and the CZT frame will be triggered and started exactly coincident with the pulse. This positions the pulse at the start of the CZT frame, and consequently one end of the window filter.
When the pulse is located at the start of a frame, the window function will reduce such a short pulse to near zero amplitude.
The Amplitude versus Time display can be used to measure short pulses. The automatic pulse measurement suite is specified to characterize pulses as short as 50 ns. Pulses shorter than 50 ns require the use of the multi-domain measurement displays.
The power trigger works on extremely short pulses. It simply looks for any digitized samples that are above the selected threshold.
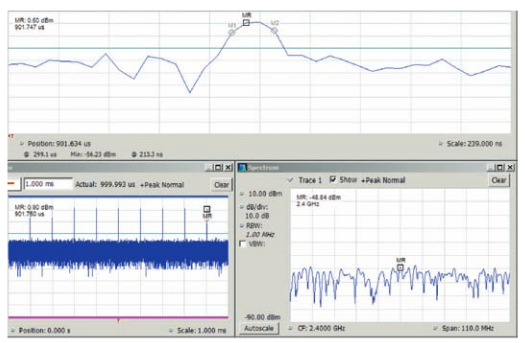
In Figure 23 the markers on the 20 ns pulse report a measurement of 19.9 ns width (with an uncertainty of 6.67 ns which is one sample time.)
The Spectrum view in the lower right has no visible spectrum. The pulse amplitude is already very low due to its narrow width. But since the pulse is at one edge of the frame, the window function has additionally reduced the amplitude below the noise.
This pulse is 20 ns long, which is a little less than one percent of one frame (which is 2.233 μs).

Figure 24 has both a non-overlapped Spectrum view and a Spectrogram view of this short duration pulse. The acquisition is triggered, so the pulse positions are every 100 μs position in the Spectrogram. There should be 13 of them visible. However, less than half are visible at all, and some of these are very low amplitude.
The marker is placed in the Spectrogram where the bottom pulse should be visible, and this selects the source for the Spectrum display on the left.
An ordinary Spectrum plot, even if triggered, may not show such a small pulse. Without overlap, the only reliable indication that some of these pulses are there, might be that the Spectrogram shows that a trigger point exists.
This is a case where overlapping transforms make the difference between no spectral visibility at all of this pulse, and great visibility. Compare Figure 24 with Figure 25.
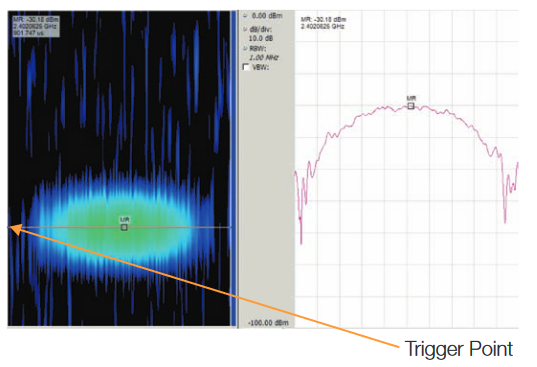
In Figure 25, the overlap has been set to start each frame 1 sample after its neighbor. There are now 174 transform frames that include some part of this pulse. Of these, there are 22 that have the pulse so close to their center that they provide measurements of the amplitude that are within 0.2 dB of each other.
The key to setting the overlap is to have enough to find the smallest pulse, or to show time-variant phenomena, but not to have more than necessary. Excess overlap causes excess time-smear of the spectral events
The marker placed in the Spectrogram display selects the one spectrum that will be displayed in the left Spectrum display. In Figure 25 both the Spectrogram and Spectrum are visible where a signal has been selected that has the pulse in the middle of the window. Only transform overlap can accomplish this.
The trigger point is in the middle of the stretched pulse. This is due to the fact that as the frames are overlapped, the position that the pulse occurs within each frame sequentially moves later in each frame by the number of sample pulses that separate each frame
Gaps in Time Lose Signals
When discrete time-to-frequency transforms are processed, the frames uses may or may not be contiguous or even overlapped. This may cause gaps in the analysis time such that a signal of interest may exist partly or entirely within such a gap. The signal may then be lost entirely.
Actual gaps
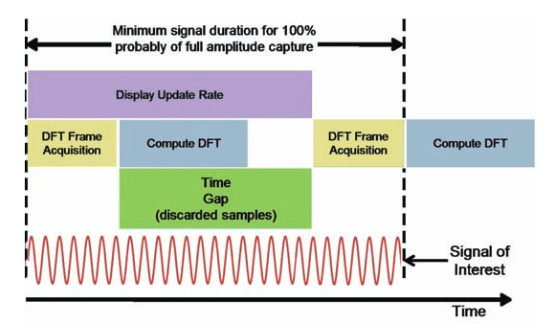
When the transform frames are separated in time with a gap between sequential frames, there is missing time in the analysis. One reason for gaps may be due to the traditional operation of a Vector Signal Analyzer, VSA, functioning as a spectrum analyzer. The frames are acquired one for each display update. Therefore, the rate at which the LCD (or other display) can update the image limits the rate of frame acquisition. Figure 26 shows this timing. The combination of the time necessary to acquire one transform frame and the transform computation time are less than the time required to update the display.
For a signal to be displayed at full amplitude, it must have duration equal to the display update rate plus one frame acquisition time. The time between frames may be very significant. During this time all incoming signals are discarded.
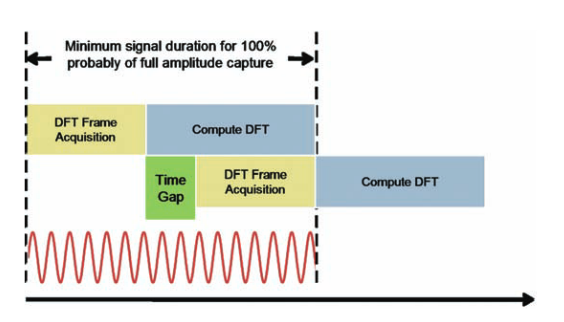
Eliminating the need to wait for the display to update for each and every transform frame allows a great reduction in the gap.The method shown in Figure 27 utilizes sequential processing of the frames. In this case the gaps are due to the transform processing time being greater than the acquisition time of a single frame.
Effective gaps
But, the Lost Samples gap may be really larger than just the difference between the computation time and the acquisition time. There is a further effective loss of samples due to the time window required by the Discrete Time Transform mathematics.
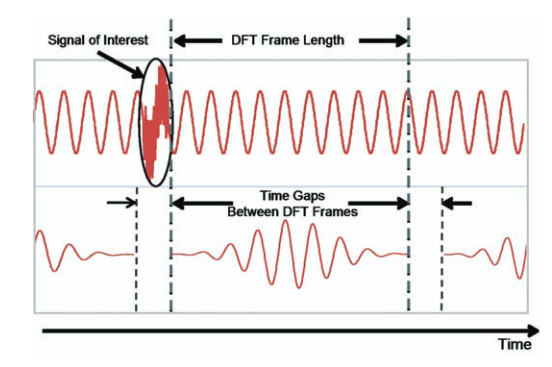
The window function reduces the samples at each end of the transform frame. This is seen in Figure 28. Here each frame has an actual gap between it and the subsequent frame where a short interference signal can be seen to be lost entirely. Note the reduction in amplitude at the ends of each frame.
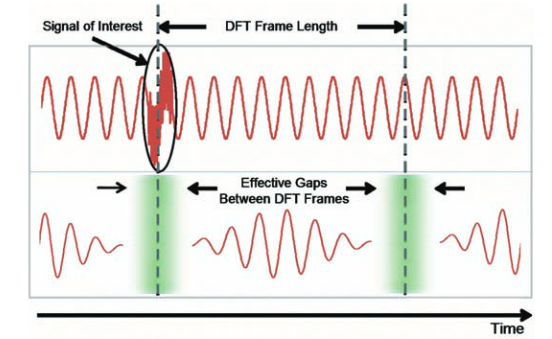
Even if the frames are directly adjacent with no samples having been discarded, there are still Effective Gaps between the frames due to the window reduction of the end amplitudes.Figure 29 demonstrates this effect. The transient interference signal is still completely lost due to landing in the middle of this Effective Gap.
Overlap – with no gaps
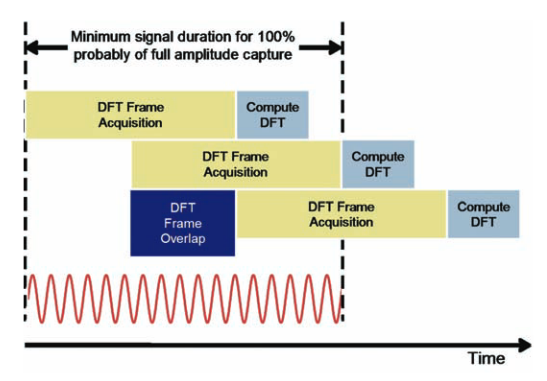
Complete elimination of the acquisition gaps and the Effective Gaps requires the use of overlapped transforms. Figure 30 shows the timing of 50% overlapped frames with a transform compute time less than the frame acquisition time. If the compute time should exceed the acquisition time, parallel compute processing will be required to maintain the 50% overlap.

Figure 31 shows the result of the 50% overlap where the short duration transient interference signal has been completely captured in one frame even though the frames on either side have completely lost it in their gap.
Digital Phosphor Spectrum View (DPX®)
Another new display of multiple time-varying RF signals is the Digital Phosphor (DPX®) Spectrum Display. This is a spectrum view with fast enough update rates that it does not miss any signal variations. Figure 32 is such a DPX display. It uses a hardware processor that (in RBW="Auto") performs 292,969 FFTs per second. Each FFT has 1024 points. The FFTs are overlapped 50% at these settings.
This display processes these FFTs in Real Time, providing a Live RF display of time-varying signals as they change. The DPX processor compresses the 292,000 spectrums per second into an update rate suitable for the LCD display used in the RSA.
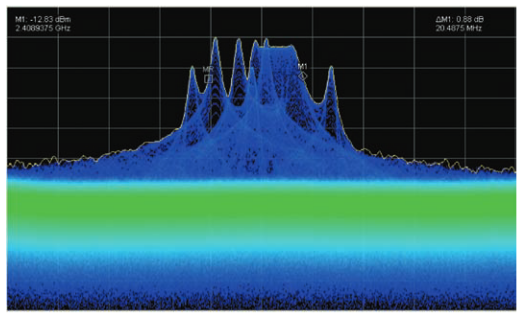
The signal originally referenced for Figure 1 is displayed using DPX in Figure 32. Here the frequency components that occur less often are dark blue, while the ones that occur more often are bright green.
The Live RF spectrum display with 50% FFT overlap will capture all events and present reduced amplitude only if the signal occupies less than one FFT frame. Even a display that uses all of the incoming A/D converter time samples in sequential FFT frames, but without overlap, will miss entirely any short events that happen to occur at the time when one FFT is ending and the subsequent one is beginning. With at least 50% overlap, there is always an FFT positioned exactly to catch spectral events that occur at the joint between any other two FFT frames.
Limitations of Overlap Processing
Overlap processing, when used for a Spectrogram, can not improve measurement resolution as much as it provides visual improvement. There is still an effective risetime limitation even if the windowing filter is removed, and there is still the timestretching effect. Both of these limitations can be overcome by using the time domain displays in the RSA to accurately measure rapid frequency changes.
Conclusion
Overlapping transforms provides a large increase in visibility of short-time varying RF phenomena. Approximately 1000 times more visibility of such events as compared to a 1024 point sequential FFT. It can show you multiple time-varying events that are shorter than the time of one transform when using the spectrogram view.
You can see extremely short pulses in a spectrogram and therefore a spectrum. You can even see pulses that are so short (20 ns or less) that when they trigger they are always at the edge of the time window and therefore not visible in the spectrum.
Overlap processing is an extremely effective time-enhancer for spectrogram.
A DPX Live RF display is another highly effective use of overlapped the FFT.
To effectively use this overlap, you must be aware of the limitations:
- Time events will appear overlapped (smeared) due to the FFT overlap
- Measurement of time within the overlap can be accurately done using the multi-domain Time or Modulation Analysis views
- Power level (or amplitude) of RF pulses or events that are shorter than one frame will appear to be lower in amplitude than they actually are. They can be accurately measured in the Power versus Time view

